Ayrılma Belitleri
Ayrılma belitleri bir topolojik uzayın üzerine konan ve noktaların ve altkümelerin birbirilerinden ne kadar ayrı olduğunu belirten belitler ailesi. Bir topolojik uzayın bu belitlerden birini sağladığı söylendiğinde, topolojisi hakkında global bir bilgi verilmiş ve topolojinin cinsi daraltılmış olur. Örneğin, topolojinin sahip olduğu açık kümelere bakmaksızın o topolojinin T0 olduğunu söylemek, topolojik uzayda seçilmiş herhangi iki noktanın birbirlerinden ayırdedilebilir olduğunu garanti eder.
Ayrılma belitleri Almanca'da ayrılma anlamına gelen Trennung sözcüğüne atıfta bulunarak T harfiyle gösterilir. Bu belitlerden bazıları çok eskiden ifade edilmiştir, bazıları daha yenidir. Kimileri çalışılan matematik dalına göre ifadesinde farklılık göstermiş ve zaman içinde şöyle böyle standart bir listeye kavuşulmuştur. Kaynağına bağlı olarak adlandırmalar farklılık gösterebilir.
Matematiksel tanımlar
X topolojik bir uzay olsun.
Eğer X'te herhangi iki nokta topolojik olarak birbirinden ayıredilebiliyorsa, yani içerildikleri açık kümeler tamamen birbirlerinin aynı değilse (yani birini içeren ve diğerini içermeyen en az bir açık küme varsa) X uzayına T0 ya da Kolmogorov denir.
Eğer birbirinden ayırdedilebilir her nokta çifti birbirinden ayrılabiliyorsa, yani birinciyi içeren ve ikinciyi içermeyen en az bir açık küme ve ikinciyi içeren ve birinciyi içermeyen en az bir açık küme varsa, X 'e R0, ya da simetrik denir.
Eğer birbirinden farklı her nokta çifti hem birbirinden ayırdedilebiliyorsa hem de ayrılabiliyorsa, X'e T1, ya da Fréchet topolojisine sahip denir. Yani T1 olmak, T0 ve R0 olmak demektir. Böyle bir uzayda tek tek noktalar birer kapalı altkümedir.
Eğer birbirinden farklı her nokta çiftinin birbirinden ayrık birer komşuluğu varsa, X'e Hausdorff, ya da T2 ya da ayrılmış denir. Bir Hausdorff uzay hem T0 hem R0'dır yani T1'dir. Fazladan istenen şey, noktaları birbirinden ayıran açık kümelerin ayrık seçilebilmesidir.
Eğer Hausdorff'luk belitinde noktaları ayıran ayrık kümeler kapalı seçilebiliyorsa, X'e T2½, ya da Urysohn denir. Tabii, tanım gereği T2½ uzay Hausdorff'tur.
Eğer verilen her kapalı küme ve onun içinde olmayan her nokta için, kümenin ve noktanın ayrık açık komşulukları bulunabiliyorsa, X'e düzenli denir.
X hem düzenli hem de T1'se, X'e düzenli Hausdorff, ya da T3 denir. Böyle bir uzay Hausdorff'tur çünkü her bir nokta kapalı bir altkümedir. Düzenli Hausdorff uzay T2½'tur.
X hem T1 uzaysa hem de verilen her kapalı K kümesi ve dışındaki her x noktası birbirinden sürekli bir fonksiyonla ayrılabiliyorsa, yani X 'ten reel sayılara K 'de 0 x 'te 1 değerini alan sürekli bir fonksiyon bulunabiliyorsa, X'e Tychonoff, ya da T3½, ya da tamamen düzenli Hausdorff denir.
Eğer verilen her kapalı ayrık küme çifti birbirilerinden açık kümelerle ayrılıyorsa, yani kapalı kümeleri içeren iki tane ayrık açık küme bulunabiliyorsa, X'e normal denir. Urysohn önsavına göre, normal bir uzayda kapalı ayrık kümeler aynı zamanda fonksiyonlarla da ayrılabilir.
X hem T1 hem de normal ise, X'e normal Hausdorff, ya da T4 denir. Urysohn önsavı, T4 uzayın T3½ olduğunu garanti eder.
X hem T1'se hem de tamamen normal ise, yani herhangi iki küme çifti açık komşuluklarıyla ayrılabiliyorsa, X'e tamamen normal Hausdorff, ya da T5 denir.
Verilen her kapalı ayrık küme çifti K ve L için, bunları birbirilerinden ayıran sürekli bir fonksiyon varsa ve bu fonksiyon altında 0'ın ters görüntüsü K, 1'in ters görüntüsü L ise, X'e mükemmel normal Hausdorff ya da T6 denir.
Yukarıda saydığımız ayrılma belitlerinin tanımdan gelen bir hiyerarşileri vardır. Listede daha başta olanlar, sonra gelenlerden daha genel durumlardır:
T0 > T1 > T2 > T2½ > T3 > T3½ > T4 > T5 > T6.
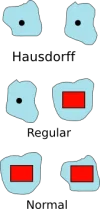
Hausdorff, düzenli (İng. regular) ve normal uzaylar. Mavi alanlar açık kümeleri, kırmızı alanlar kapalı kümeleri, kara yuvarlaklar noktaları temsil ediyor.
Ayrılma belitleri bir topolojik uzayın üzerine konan ve noktaların ve altkümelerin birbirilerinden ne kadar ayrı olduğunu belirten belitler ailesi. Bir topolojik uzayın bu belitlerden birini sağladığı söylendiğinde, topolojisi hakkında global bir bilgi verilmiş ve topolojinin cinsi daraltılmış olur. Örneğin, topolojinin sahip olduğu açık kümelere bakmaksızın o topolojinin T0 olduğunu söylemek, topolojik uzayda seçilmiş herhangi iki noktanın birbirlerinden ayırdedilebilir olduğunu garanti eder.
Ayrılma belitleri Almanca'da ayrılma anlamına gelen Trennung sözcüğüne atıfta bulunarak T harfiyle gösterilir. Bu belitlerden bazıları çok eskiden ifade edilmiştir, bazıları daha yenidir. Kimileri çalışılan matematik dalına göre ifadesinde farklılık göstermiş ve zaman içinde şöyle böyle standart bir listeye kavuşulmuştur. Kaynağına bağlı olarak adlandırmalar farklılık gösterebilir.
Matematiksel tanımlar
X topolojik bir uzay olsun.
Eğer X'te herhangi iki nokta topolojik olarak birbirinden ayıredilebiliyorsa, yani içerildikleri açık kümeler tamamen birbirlerinin aynı değilse (yani birini içeren ve diğerini içermeyen en az bir açık küme varsa) X uzayına T0 ya da Kolmogorov denir.
Eğer birbirinden ayırdedilebilir her nokta çifti birbirinden ayrılabiliyorsa, yani birinciyi içeren ve ikinciyi içermeyen en az bir açık küme ve ikinciyi içeren ve birinciyi içermeyen en az bir açık küme varsa, X 'e R0, ya da simetrik denir.
Eğer birbirinden farklı her nokta çifti hem birbirinden ayırdedilebiliyorsa hem de ayrılabiliyorsa, X'e T1, ya da Fréchet topolojisine sahip denir. Yani T1 olmak, T0 ve R0 olmak demektir. Böyle bir uzayda tek tek noktalar birer kapalı altkümedir.
Eğer birbirinden farklı her nokta çiftinin birbirinden ayrık birer komşuluğu varsa, X'e Hausdorff, ya da T2 ya da ayrılmış denir. Bir Hausdorff uzay hem T0 hem R0'dır yani T1'dir. Fazladan istenen şey, noktaları birbirinden ayıran açık kümelerin ayrık seçilebilmesidir.
Eğer Hausdorff'luk belitinde noktaları ayıran ayrık kümeler kapalı seçilebiliyorsa, X'e T2½, ya da Urysohn denir. Tabii, tanım gereği T2½ uzay Hausdorff'tur.
Eğer verilen her kapalı küme ve onun içinde olmayan her nokta için, kümenin ve noktanın ayrık açık komşulukları bulunabiliyorsa, X'e düzenli denir.
X hem düzenli hem de T1'se, X'e düzenli Hausdorff, ya da T3 denir. Böyle bir uzay Hausdorff'tur çünkü her bir nokta kapalı bir altkümedir. Düzenli Hausdorff uzay T2½'tur.
X hem T1 uzaysa hem de verilen her kapalı K kümesi ve dışındaki her x noktası birbirinden sürekli bir fonksiyonla ayrılabiliyorsa, yani X 'ten reel sayılara K 'de 0 x 'te 1 değerini alan sürekli bir fonksiyon bulunabiliyorsa, X'e Tychonoff, ya da T3½, ya da tamamen düzenli Hausdorff denir.
Eğer verilen her kapalı ayrık küme çifti birbirilerinden açık kümelerle ayrılıyorsa, yani kapalı kümeleri içeren iki tane ayrık açık küme bulunabiliyorsa, X'e normal denir. Urysohn önsavına göre, normal bir uzayda kapalı ayrık kümeler aynı zamanda fonksiyonlarla da ayrılabilir.
X hem T1 hem de normal ise, X'e normal Hausdorff, ya da T4 denir. Urysohn önsavı, T4 uzayın T3½ olduğunu garanti eder.
X hem T1'se hem de tamamen normal ise, yani herhangi iki küme çifti açık komşuluklarıyla ayrılabiliyorsa, X'e tamamen normal Hausdorff, ya da T5 denir.
Verilen her kapalı ayrık küme çifti K ve L için, bunları birbirilerinden ayıran sürekli bir fonksiyon varsa ve bu fonksiyon altında 0'ın ters görüntüsü K, 1'in ters görüntüsü L ise, X'e mükemmel normal Hausdorff ya da T6 denir.
Yukarıda saydığımız ayrılma belitlerinin tanımdan gelen bir hiyerarşileri vardır. Listede daha başta olanlar, sonra gelenlerden daha genel durumlardır:
T0 > T1 > T2 > T2½ > T3 > T3½ > T4 > T5 > T6.

Hausdorff, düzenli (İng. regular) ve normal uzaylar. Mavi alanlar açık kümeleri, kırmızı alanlar kapalı kümeleri, kara yuvarlaklar noktaları temsil ediyor.

