Brocard noktaları, geometride bir üçgen içinde yer alan özel noktalardır. Fransız matematikçi Henri Brocard'ın çalışmalarından dolayı bu adı almıştır.
Tanım
Kenarları a, b ve c, köşeleri saat yönünün tersine doğru A, B ve C olarak adlandırılmış bir ABC üçgeninde, AP, BP ve CP sırasıyla c, a ve b kenarlarıyla eşit ω açısı yapacak şekilde bir P noktası bulunur.
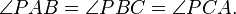 Bu P noktasına ABC üçgeninin birinci Brocard noktası ve ω açısına üçgenin Brocard açısı denir. Bu açı şu denklemi sağlar:
Bu P noktasına ABC üçgeninin birinci Brocard noktası ve ω açısına üçgenin Brocard açısı denir. Bu açı şu denklemi sağlar:
 ABC üçgeninde AQ, BQ ve CQ doğru parçalarının sırasıyla b, c ve a kenarlarıyla eşit açı yapması şartını sağlayan bir Q, ikinci Brocard noktası, bulunur. Diğer bir deyişle
ABC üçgeninde AQ, BQ ve CQ doğru parçalarının sırasıyla b, c ve a kenarlarıyla eşit açı yapması şartını sağlayan bir Q, ikinci Brocard noktası, bulunur. Diğer bir deyişle
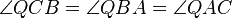 denklemi bu nokta için de geçerlidir. Dikkat çekici biçimde, bu ikinci Brocard noktası ile birinci Brocard noktası aynı Brocard açısına sahiptir. Yani
denklemi bu nokta için de geçerlidir. Dikkat çekici biçimde, bu ikinci Brocard noktası ile birinci Brocard noktası aynı Brocard açısına sahiptir. Yani
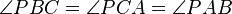 ve
ve
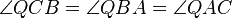 birbirine eşittir.
birbirine eşittir.
İki Brocard noktası arasında yakın ilişki vardır; aslında ikisi arasındaki fark ABC üçgeninin açılarının hangi sırayla seçildiğine bağlıdır. Örnek verilirse, ABC üçgeninin birinci Brocard noktası, ACB üçgeninin ikinci Brocard noktasıdır.
ABC üçgeninin iki Brocard noktası birbirinin izogonal eşleniğidir.
Elde edilmesi
Brocard noktalarını oluşturmanın en iyi yolu için şöyle denebilir. Verilecek örnekte sadece birinci Brocard noktası ele alınacak ancak ikinci Brocard noktasını bulmak buna çok benzerdir.
A ile B noktalarından geçen, üçgenin BC kenarına teğet bir çember (bu çemberin merkezi AB'nin ortadikmesi ile B noktasından BC'ye dik olarak çizilecek doğrunun kesişim noktası olacaktır) oluşturulur. Simetrik olarak, B ile C noktalarından geçen, AC kenarına teğet ve A ile C noktalarından geçen, AB kenarına teğet çemberler çizilir. Bu üç çemberin ortak tek noktası, ABC üçgeninin birinci Brocard noktasıdır.
İkinci Brocard noktası aynı yöntemle tespit edilebilir.
Tanım
Kenarları a, b ve c, köşeleri saat yönünün tersine doğru A, B ve C olarak adlandırılmış bir ABC üçgeninde, AP, BP ve CP sırasıyla c, a ve b kenarlarıyla eşit ω açısı yapacak şekilde bir P noktası bulunur.
İki Brocard noktası arasında yakın ilişki vardır; aslında ikisi arasındaki fark ABC üçgeninin açılarının hangi sırayla seçildiğine bağlıdır. Örnek verilirse, ABC üçgeninin birinci Brocard noktası, ACB üçgeninin ikinci Brocard noktasıdır.
ABC üçgeninin iki Brocard noktası birbirinin izogonal eşleniğidir.
Elde edilmesi
Brocard noktalarını oluşturmanın en iyi yolu için şöyle denebilir. Verilecek örnekte sadece birinci Brocard noktası ele alınacak ancak ikinci Brocard noktasını bulmak buna çok benzerdir.
A ile B noktalarından geçen, üçgenin BC kenarına teğet bir çember (bu çemberin merkezi AB'nin ortadikmesi ile B noktasından BC'ye dik olarak çizilecek doğrunun kesişim noktası olacaktır) oluşturulur. Simetrik olarak, B ile C noktalarından geçen, AC kenarına teğet ve A ile C noktalarından geçen, AB kenarına teğet çemberler çizilir. Bu üç çemberin ortak tek noktası, ABC üçgeninin birinci Brocard noktasıdır.
İkinci Brocard noktası aynı yöntemle tespit edilebilir.
