Nitelikler
Bağımsızlık
Bir doğrusal denklem dizgesinin denklemleri bağımsızlık niteliği, dizgede bulunan denklem eşitliklerinin hiçbiri denklemden cebirsel olarak çıkartılaması halidir. Eğer denklemler bağımsızlarsa, her bir denklem değişkenler hakkında yeni bilgi kapsamaktadır, ve bu denklemlerden herhangi birinin ortadan kaldırılması çözüm kümesinin boyutunu artır. Doğrusal denklemler için mantıksal bağımsızlık doğrusual bağımsızlık özelliğiyle ile aynıdır.

x1 − 2x2 = − 1, 3x1 + 5x2 = 8 ve 4x1 + 3x2 = 7 denklemleri doğrusal olarak bağımsız değildirler.
Örneğin, şu denklemler

bağımsız değildirler; çünkü ikinci denklem birinci denklemin 2 ile çarpımı ile elde edilmiştir ve eğer bu iki denklem için grafik çizilirse iki doğru üste çakışıp tek bir doğru görüntüsü verirler.
Daha karmsaik bir örneğin için verilen denklemler dizgesi şu olsun:
Bu üç denklem dizgesi bağımsız değildir, çünkü üçüncü denklem ilk iki denklemin birbirine toplkamından elde edilmiştir. Gerçekten bu üç denklemden herhangi ikisinden üçüncü denklem çıkartılabilir ve bu üç denklemden herhangi tek bir tanesi ortadan kaldırılırsa çözüm kümesi hiç değişmeden aynı kalır. Bu üç doğru için grafik üçü de tek bir noktada kesişen üç doğru şeklindedir.
Tutarlılık
Bir doğrusal denklemler dizgesi denklemleri, eğer bir ortak çözüm varsa, "tutarlı" olur; aksi halde "tutarsız" olur. Eğer denklemler tutarlı iseler; denklemlerden bir çelişkilik ortaya çıkartmak imkanı bulunur; örneğin 1 = 3 ifadesi gibi.
Örneğin şu denklemler

tutarsızdır. Bir çözüm bulmaya çalışmak için, söylenmeden anlaşılan "bir çözüm vardır" varsayımını yapmaktayız. Diğer bir ifade ile, birinci denklemmde bulunan x1 değerinin ikinci denklemde bulunan x1 değeri ile aynı açıkça olduğunu açıkça söylemeden varsaymaktayız (ve aynı şekilde ve aynı zamanda her iki denklemde de x2 aynı varsayımı yapıyoruz.) (3x1 + 2x2 ıcın ikame ediliebilirlik özelliğini uyguluyarak 6 = 12 olarak bir denklem buluruz ve bu da yanlış bir ifadededir. Bu hatalı ifade dizgenin bir çözümü olduğuna dair yaptımız varsayım ile çelişmektedir ve bundan dolayı varsayımımızın yanlış olduğu sonucu çıkmaktadır; yani doğrusal denklemler dizgesinin "hiçbir çözümü bulunmaz". Bu denklemlerin x1x2 düzeyindeki grafikleri birbirine parallel iki doğru halindedir.
Üç doğrusal denklemli dizgede, bu dizgedeki herhengi iki denklem birlirleriyle tutarlı olmalarıyla beraber, denklemlerin tutarsız olmaları mümkündür. Örneğin şu denklemler tutarsızdır:

Birinci ile ikinci denklemin birbiriyle toplamaları ile
3x1 + 2x2 = 2
elde edilir ve bu üçüncü denkelmeden çıkartılırsa sonuç
0 = 1
olur. Dikkat edilirse bu denklemlerden herhangi bir iki denklemli dizgenin bir ortak çözümü vardır. Aynı olgu her türlü sayıda denkelemler dizgesinde de oluşabilir.
Genel bir sonuç olarak, eğer bir doğrusal denklemler dizgesindeki denklemlerin sol tarfındaki ifadeler doğrusal olarak bağımlı olursa ve sabit terimler bağımlılık bağlantısını tatmin etmiyorlarsa, tutarsızlık ortaya çıkar. Eğer bir doğrusal denklemler dizgesinin sol tarafındaki ifadeler doğrusal olarak bağımsızlarsa, bu dizge her zaman tutarlı olur.
Denklik
Aynı değişkenleri kullanan iki değişik doğrusal denklemler dizgesinin birbirleriye denk olması için ikinci dizgede bulunan denklemlerin herbirinin, birinci dizgede bulunan denklemlerden cebir kullanılarak hesaplanıp elde edilebilmesi gerekir ve bunun aksinin de doğru olması gereklidir. Birbirine denk dizgeler değişken değerleri hakkında birbirine tıpatıp aynı bilgileri vermektedirler. Özellikle, eğer iki dizgenin tıpatıp aynı çözüm kümesi bulunuyorsa iki doğrusal denklemler dizgesi birbirlerine denktirler.
Doğrusal denklemler dizgesinin çözümü [değiştir]
Bir doğrusal denklem dizgesini çözümlemek için birkaç değişik denklem çözümleme algoritması bulunur.
Çözümü tanımlama
Eğer çözüm kümesi sonsuz değilse, genellikle bu küme olarak ve küme notasyonu kullanarak ifade edilir. Örneğin 2, 3, 4 olan çözüm kümesi {2,3,4} olrak yazılır.
Eğer sonsuz sayıda çözüm bulunuyorsa bunu küme olarak ve küme notasyonu kullanarak ifade etmek çok güç olur. Tipik olarak değişkenlerden bazıları bağımsız (veya özgür veya parametre) olarak kabul edilirler ve herhangi bir değer alabilirler. Geride kalan değişkenler bağımsız değişkenlerin değerlerine bağlı olurlar.
Örneğin şu dizgeye ele alalım:

Bu dizge için çözüm kümesi şu denklemeler ile ifade edilebilir:

Burada x3 bağımsız değişkendir; x1 ve x2 değişkenleri x3ye bağlıdırlar. Çözüm kümesinde bulunan herhangi nokta önce x3 için herhangi bir değer seçmekle ve sonra da x1 ve x2 için bu seçilen değere tekabül eden değerleri hesaplama şeklinde ortaya çıkartılır.
Her bir bağımsız değişken çözüm kümesine bir serbestlik derecesi verir ve serbestlik derecesi sayısı çözüm kümesinin boyutuna eşittir. Örneğin, yukarıda verilen denklemin çözüm kümesi bir doğru olur; çünkü çözüm kümesi üzerinde bulunan tek bir nokta x3 parametre değişkenin değerini şahsi seçime bağlı olarak belirlemek suretiyle ortaya çıkartılır. Daha yüksek düzenli sonsuz sayıda çözüm bir düzlemi veya yüksek boyutlu hiperdüzlemi tanımlayabilir.
Bağımsız değişkenler için değişik seçim değerleri, aynı çözüm kümesinin değişik tanımlarını oratay çıkarabilir. Örneğin yukarıda verilen denklemlerin çözümü alternatif olarak şöyle değişik şekilde tanımlanabilir:

Burada x1 bağımsız değişken ve x2 ve x3 bağlı değişkenlerdir.
Değişkenlerin arkaarkaya eliminasyonu
Bir doğrusal denklemler dizgesine çözüm kümesi bulmak için en basit yöntem değişkenlerin tekere teker arkaarkaya elimine edilmesidir. Bu çözüm yöntemi şöyle tanımlanabilir:
Birinci denklemdeki tek bir değişkeni (eşit işaretinin solunda) diğer değişkenler ve sabitle (sağda) ifade edilmesini sağlayınız.
Bu değişken için birinci denkelmeden bulunan ifadeyi dizgenin diğer denklemelerinde bulunan ifadeleri içindeki o değişken yerine konulur ve böylece yeni bir denklemler dizgesi bulunur ve bu dizgede bir önce dizgeden bir değişken eksik olur.
Bu yeni dizgeye aynı yöntemi uygulayınız, Böylece tekrar bir değişken eksik yeni bir dizge bulunuz.
Bu yöntemi arkaarkaya uygulayınız ve son bulunan dizge tek bir doğrusal denklem olana kadar bir yöntemi uygulamaya devam ediniz.
Bu son tek değişkenli denklemi çözünüz ve bu son değişkenin çözüm değerini bulunuz.
Bu değeri diğer bir öneceki dizgede geriye koyup bir diğer değişkenin çözüm değerini bulun. Bu geriye koyup çözmeyi tüm değişkenler için çözüm bulana kadar tekrarlayınız.
Örneğin şu 3 değişkenli (x, y ve z) doğrusal denklemeler dizgesini ele alalım :
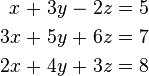
Birinci deklemi x için çözelim ve şu ifadeyi elde ederiz;
x = 5 + 2z − 3y
Bu x için ifadeyi ikinci ve üçüncü doğrusal denkleme koyup bunları basitleştirelim ve şu iki değişkenli (y ve z) iki denklem bulunuruz:

Bu yeni iki değişkenli iki denklemli dizgenin birinci denklemini y için çözelim ve şu ifadeyi elde ederiz
y = 2 + 3z,
Bunu yeni dizgedeki ikinci denkleme koyalım. y için çözünce şu ifade elde edilir:
y = 2 + 3z
Bunu ikinci denkleme y için koyarsak
z = 2
ifadesini elde ederiz. Şimdi sadece z ifadeli tek doğrusal denklem dizge elimizde kalmıştır ve bu da z için şu çözümü verir:
z = 2
Arkaarkaya tek değişken eliminasyonu ile sonuçlar bulmuştuk:
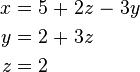
Şimdi z = 2 çözümünü ikinci denkelem koyarsak y çözümü olarak y = 8
elde ederiz; ve z = 2 ile y = 8 çözümlerini birinci denkleme koyarsak
x = −15
olarak x çözümü bulunur.
Böylece, çözüm kümesi olarak tek bir nokta olan (x, y, z) = (−15, 8, 2) elde edilmiş olmaktadır.