Cramer kuralı
Bu kural 1750'de "Introduction à l'analyse des lignes courbes algébriques (Cebirsel eğrilerinin analizine giriş)" adlı eserinde bu teoremi açıklayan Gabriel Cramer (1704–1752) anısına isimlendirilmiştir.
Cramer kuralı aynı sayıda değişken ile denklem bulunan doğrusal denklem dizgesinin çözüm kümesini bulmak için kullanılabilen bir ifade ortaya çıkaran bir doğrusal cebir teoremidir. Bu teorem kullanılarak çözüm tek ve tek bir çözüm kümesi bulunan doğrusal denklem dizgesi için geçerlidir. Bu halde her bir değişken için çözüm iki kare determinantın oranı olarak verilir; bu oranda pay katsayılar matrisinden o değişkene karşıt sütununun, denklemin sağ-tarafında olan sabitler vektörü ile ikame edilmesiyle elde edilen kare matrisin determinantı ve payda ise katsayılar kare matrisi determinantıdır.
Genel olarak açıklamak için aynı sayıda (n) değişkenli ve denklemli bir doğrusal denklemler dizgesinin şu matris ifadesini ele alalım:
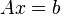

Burada A matrisi (nxn) seviyeli sonsuz değeri olmayan bir determinanti bulunan bir "katsayılar (kare) matrisi";

seviyeli bir "degiskenler (sutun) vektoru"; ve
seviyeli bir "sabitler (sutun) vektoru" olur.
xideğişkeni çözümü için Cramer Teoremi şöyle ifade edilir:

Burada Ai matrisi A kare matrisinin i'inci sütununun yerine b sütun matrisinin konulmuş olduğu matrisdir.