Geometrik Kavramlar

Geometride “Nokta”, “Doğru”, “Düzlem” gibi kavramlar tanımsız olarak kabul edilir.

1. Nokta: “.” biçiminde gösterilir. Boyutu yoktur.

2. Doğru: İki uçtan sınırsız noktalar kümesidir.


3. Düzlem: Her yönde sonsuza giden noktalar kümesidir.

E düzlemi dört yönde de sonsuza kadar gider.
E düzlemi yandaki gibi gösterilir.

4. Doğru Parçası: İki nokta ile bu iki nokta arasında kalan noktaların birleşimidir.

[AB] sembolüyle gösterilir.
[AB] ® AB doğru parçası
|AB| ® AB doğru parçasının uzunluğu

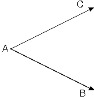
5. Işın: Bir başlangıç noktası olup sonsuza giden noktalar kümesidir.

[AB ® AB ışını

6. Yarı Doğru: [AB ışınından A noktasının çıkarılması ile elde edilen kümeye AB yarıdoğrusu denir.

]AB sembolüyle gösterilir.

Doğrusal nokta kümelerinin gösterimi




AÇILAR
Başlangıç noktaları ortak iki ışının birleşimine açı denir.
şekilde [AC ve [AB ışınının oluşturduğu açı BAC açısıdır.

[ABÈ[AC = BAC açısıdır.BAC, CAB olarak veya A ile gösterilir.

[AB ve [AC ışınları açının kenarları,
A noktası açının köşesidir.

Açı yazılırken açının köşesi olan nokta ortada yazılır.

1. Açının Ölçüsü

[AB ile [AC arasındaki açıklığın ifadesine açının ölçüsü denir. BAC açısının ölçüsü a dır.m(BAC) = a veya m(A) = a olarak gösterilir.

ölçüleri eşit olan açılara eş açılar denir.

2. Açının Düzlemde Ayırdığı Bölgeler
Bir açı düzlemi üç bölgeye ayırır.

a. Açının kendisi
[AB ve [AC ışınları.

b. İç bölge (taralı alan)
c. Dış bölge

3. Açı ölçü birimleri
Açı ölçüsü birimi olarak genelde derece kullanılır. Dereceden başka Grad ve Radyan birimleri de kullanılır. Açı ölçüsü birimleri arasında,

360° = 400 G(grad) = 2p (radyan) eşitliği vardır.
Bir ışının başlangıç noktası etrafında bir tur döndürülmesi ile elde edilen açı 360° dir.

Derecenin alt birimleri

1° = 60' (dakika)
1' = 60" (saniye)
1° = 3600" dir.
90° = 89° 59' 60" ve
180° = 179° 59' 60" olur.

4. Ölçülerine göre açılar
a. Ölçüsü 0° ile 90° arasında olan açılara dar açı denir.


b. Ölçüsü 90° olanaçılara dik açı denir


c. Ölçüsü 90° ile 180° arasında olan açılara geniş açı denir.


d. Ölçüsü 180° olan açılara doğru açı denir


e. Ölçüsü 360° olan açıya tam açı denir.

5. Komşu açılar
Köşeleri ve birer ışınları ortak olan, iç bölgesi ortak olmayan açılara komşu açılar denir.CAD ile DAB komşu açılardır.



6. Açıortay
Açıyı iki eşit parçaya bölen ışına açıortay denir.[AD, CAB açısının açıortayıdır.Açıortay üzerinde alınan her noktanın açının kollarına olan dik uzaklıkları eşittir.



7. Tümler açı
Ölçüleri toplamı 90° olan iki açıya tümler açılar denir.

m(CAD)+m(DAB)=90° a+b=90°
a
açısının tümlerinin ölçüsü (90° – a) dır.

Komşu tümler iki açının açıortay doğruları arasındaki açının ülçüsü 45° dir.

[OA] ^ [OB]m(KOL) = 45°


8. Bütünler açı
Ölçüleri toplamı 180° olan iki açıya bütünler açılar denir.

m(DAB)+m(CAD)=180° x+y=180°
x açısının bütünlerinin ölçüsü (180° – x) dir.

Komşu bütünler iki açının açıortay doğruları arasındaki açının ölçüsü 90° dir.

m(KOL) = 90°


9. Ters Açılar
Kesişen iki doğrunun oluşturduğu açılardan komşu olmayanlara ters açılar denir.

Ters açıların ölçüleri eşittir.



m(x)=m(z) ve

m(t)=m(y) dir.

10. Paralel iki doğrunun bir kesenle yaptığı açılar

a. Yöndeş açılar

d1 // d2 ise


Yöndeş açıların ölçüleri eşittir.
m(a) = m(x) ; m(b) = m(y)

m(c) = m(z) ; m(d) = m(t)


b. İçters açılar

d1 // d2 ise a ile z ve b ile t içters açılarıdır.


İçters açıların ölçüleri eşittir.
m(a) = m(z); m(b) = m(t)


Dışters açılar

d1 // d2 ise


Dışters açıların ölçüleri eşittir.
m(c)=m(x)=m(d)=m(y)


d. Karşı durumlu açılar

d1 // d2 ise


Karşı durumlu açıların toplamı 180° dır.
m(a) + m(t) = 180°; m(b) + m(z) = 180°


Karşı durumlu açıların açıortayları arasındaki açının ölçüsü 90° dir.

Paralel doğrular arasında birden fazla kesenin olduğu durumlarda kesişim noktalarından yeni paraleller çizilir.


e. Birden fazla kesenli durumlar

d₁ // d₂ ise B noktasından d₁ ve d₂ doğrularına paralel çizersek m(ABC) = a + b olur.


B noktasından paralel çizersek m(ABD) + x = 180°m(DBC) + z = 180° buradanx + y + z = 360° dir.



f. Paralel doğrular arasındaki ardışık zıt yönlü açılar



d1 // d2ise a + b + c = x + y olur.Bu tür soruları kırılma noktalarından paralellerçizerek de çözebiliriz.


g. Kolları paralel ve kolları dik açılar

Açıları oluşturan ışınlar aynı yönde ve paralel ise bu iki açının ölçüsü eşittir.


Açıları oluşturan ışınlar zıt yönlü ve paralel ise bu iki açının ölçüsü eşittir.


Açıları oluşturan ışınlardan biri aynı diğeri zıt yönlü ve paralel ise bu iki açının ölçüleri toplamı;a + b = 180° olur.


Kenarları birbirine dik karşılıklı iki açının ölçüleri toplamıa + b = 180° olur.


Kenarları şekildeki gibi birbirine dik açıların ölçüleri eşittir.

Geometrik kavramlarla ilgili görüş ve önerilerinizi konu altında belirtebilirsiniz.