Küre nedir?
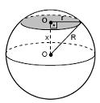
Uzayda sabit bir noktaya esit uzaklıkta olan noktaların kümesine küre denir.
Küre;
Kürenin yüzey alanı = 4. pi. R2
Kürenin hacmi = 4. pi. R3 / 3
Bir küre, merkezinden x birim uzaklıkta kesildiginde, olusan kesit yüzeyi bir dairedir.
Taralı alan = pi.r2 dir
Koni nedir?
Tabanı daire olan piramittir.
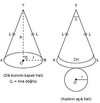
Dik koni
Yüksekligi taban merkezinden geçen koniye dik koni veya dönel koni denir.
Koni;
Yanal alanı = pi. r.L
Bütün alan= pi. r.L + pi. r2
Koninin hacmi = pi.r2.h / 3
Kesik koni
Kesik koninin hacmi= [ (h-h1). pi /3 ] .( r2 + r12 + r.r1 )
Yandaki küçük koni ile tüm koni benzerdir.Kesik koninin hacmi, tüm koni ile üstteki koninin farkı düsünülerek formül
kullanılmadan da bulunabilir.
Piramit nedir?
Bir düzlemde bulunan bir çokgen ile bu düzlemin dısında bir T noktası alalım. T noktası ile bu çokgenin tüm noktaları birlestirildiginde olusan cisme piramit denir.
Kare Piramit
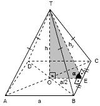
Tabanı düzgün çokgen ve yüksekligi taban merkezinden geçen piramittir.
Yan ayrıtları esittir.
|TA| = |TB| = |TC| = |TD|
|OT| = h (piramidin yüksekligi)
|TE| = hy (yanal yükseklik)
m(TEO) = alfa° (yaz yüzün taban düzlemi ile yaptıgı açı)
Yanal Alanı = (taban çevresi).(yanal yükseklik) / 2
Hacmi= (Taban Alanı).(yükseklik) / 3
Eşkenar Üçgen Pramit
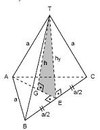
Bütün yüzleri eskenar üçgen olan piramide düzgün dörtyüzlü denir.
duzgun-dortyuzlu
G, ABC üçgeninin agırlık merkezidir.
|TG| = h = ( a√6 ) / 3 (yükseklik)
|TE| = hy = ( a√3 ) / 2 (yanal yükseklik)
Alan = a2 √3
Hacmi = ( a3 √2 ) / 12
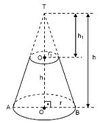
Silindir nedir
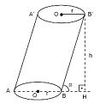
Tabanı daire olan prizmaya silindir denir.
[B'H] = h (egik silindirin yüksekligi)
[AA'] = [BB'] (Ana dogrular)
Hacmi = pi. r2. h
alfa açısı = Yan yüzün taban düzlemi ile yaptıgı açıdır.
Dik Silindir
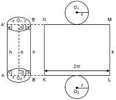
Ana dogruları tabana dik olan silindire dik silindir veya dönel silindir denir.
Yan yüzün açılımı KLMN dikdörtgeni olduguna göre
Yanal alant = 2.pi. r.h
Bütün alan = 2.pi. r.h + 2.pi. r2
Hacmi = pi.r2.h
Bütün yüzleri kare olan bir prizmadır.
Küp
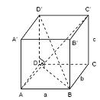
Alan = S = 6a2
Hacim = v = a3
Cisim kösegeni = |BD’| = |AC’| = a √a
Bütün yüzleri dikdörtgen olan prizmadır.
Dikdortgenler Prizması
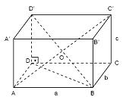
Dikdörtgenler prizmasının özellikleri
Alani = S = 2 (ab + ac + bc)
Hacmi = V = a. b . c
Cisim Kösegeni: |AC‘| = |BD’| = alt
|AO| = |BO| = |C’O| = |D’O| dur.

Uzayda sabit bir noktaya esit uzaklıkta olan noktaların kümesine küre denir.
Küre;
Kürenin yüzey alanı = 4. pi. R2
Kürenin hacmi = 4. pi. R3 / 3
Bir küre, merkezinden x birim uzaklıkta kesildiginde, olusan kesit yüzeyi bir dairedir.
Taralı alan = pi.r2 dir
Koni nedir?
Tabanı daire olan piramittir.

Dik koni
Yüksekligi taban merkezinden geçen koniye dik koni veya dönel koni denir.
Koni;
Yanal alanı = pi. r.L
Bütün alan= pi. r.L + pi. r2
Koninin hacmi = pi.r2.h / 3
Kesik koni

Kesik koninin hacmi= [ (h-h1). pi /3 ] .( r2 + r12 + r.r1 )
Yandaki küçük koni ile tüm koni benzerdir.Kesik koninin hacmi, tüm koni ile üstteki koninin farkı düsünülerek formül
kullanılmadan da bulunabilir.
Piramit nedir?
Bir düzlemde bulunan bir çokgen ile bu düzlemin dısında bir T noktası alalım. T noktası ile bu çokgenin tüm noktaları birlestirildiginde olusan cisme piramit denir.
Kare Piramit

Tabanı düzgün çokgen ve yüksekligi taban merkezinden geçen piramittir.
Yan ayrıtları esittir.
|TA| = |TB| = |TC| = |TD|
|OT| = h (piramidin yüksekligi)
|TE| = hy (yanal yükseklik)
m(TEO) = alfa° (yaz yüzün taban düzlemi ile yaptıgı açı)
Yanal Alanı = (taban çevresi).(yanal yükseklik) / 2
Hacmi= (Taban Alanı).(yükseklik) / 3
Eşkenar Üçgen Pramit

Bütün yüzleri eskenar üçgen olan piramide düzgün dörtyüzlü denir.
duzgun-dortyuzlu
G, ABC üçgeninin agırlık merkezidir.
|TG| = h = ( a√6 ) / 3 (yükseklik)
|TE| = hy = ( a√3 ) / 2 (yanal yükseklik)
Alan = a2 √3
Hacmi = ( a3 √2 ) / 12
Silindir nedir

Tabanı daire olan prizmaya silindir denir.
[B'H] = h (egik silindirin yüksekligi)
[AA'] = [BB'] (Ana dogrular)
Hacmi = pi. r2. h
alfa açısı = Yan yüzün taban düzlemi ile yaptıgı açıdır.
Dik Silindir

Ana dogruları tabana dik olan silindire dik silindir veya dönel silindir denir.
Yan yüzün açılımı KLMN dikdörtgeni olduguna göre
Yanal alant = 2.pi. r.h
Bütün alan = 2.pi. r.h + 2.pi. r2
Hacmi = pi.r2.h
Bütün yüzleri kare olan bir prizmadır.
Küp

Alan = S = 6a2
Hacim = v = a3
Cisim kösegeni = |BD’| = |AC’| = a √a
Bütün yüzleri dikdörtgen olan prizmadır.
Dikdortgenler Prizması

Dikdörtgenler prizmasının özellikleri
Alani = S = 2 (ab + ac + bc)
Hacmi = V = a. b . c
Cisim Kösegeni: |AC‘| = |BD’| = alt
|AO| = |BO| = |C’O| = |D’O| dur.


