Holomorfik Fonksiyon
Holomorfik fonksiyonlar karmaşık analizin temel çalışma araçlarından biridir. Bu fonksiyonlar karmaşık düzlemin yani C'nin açık bir altkümesinde tanımlı, bu altkümedeki her noktada karmaşık anlamda türevli ve aldığı değerler yine C içinde olan fonksiyonlardır. Bu koşul normal gerçel türevlilikten daha güçlüdür. Daha derin anlamda, holomorfik fonksiyon sonsuz kere türevlenebilir ve Taylor serisi ile tanımlanabilir. Her ne kadar daha geniş anlamda (gerçel, karmaşık veya daha genel bir çerçevede) fonksiyonun tanım kümesi içindeki her noktanın komşuluğunda fonksiyonun Taylor serisine eşit olması anlamına gelse de, analitik fonksiyon teriminin holomorfik fonksiyon terimi yerine de kullanıldığı bolca yer vardır. Analitik fonksiyonlar sınıfının karmaşık analizde holomorfik fonksiyonlar sınıfı ile aynı olması karmaşık analizde önemli bir teoremdir. Holomorfik fonksiyonlara bazen kümesine ait bir düzenli fonksiyonlar dendiği de olmaktadır. Karmaşık düzlemin tümünde holomorfik olan fonksiyona tam fonksiyon adı verilir. "a noktasında holomorfik olma" terimi a noktasında türevli manasına gelmekle beraber aynı zamanda karmaşık düzlemde a noktası etrafındaki belli bir açık disk içindeki her noktada türevli anlamına da gelmektedir.
Tanım
U kümesi C 'nin açık bir kümesiyse, f : U → C, U üzerinde tanımlı karmaşık bir fonksiyonsa ve Uzo noktasındaki
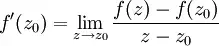
limiti varsa, f 'ye z0 noktasında karmaşık türevli denilir. Burada limit z0 noktasına yaklaşan karmaşık sayıların tüm dizileri üzerinden alınır ve bu tür tüm diziler için farkların oranı tek bir sayıya yaklaşmak zorundadır ki o sayı da f '(zo) 'dır. Sezgisel olarak, f fonksiyonu zo 'da karmaşık türevliyse ve zo 'a r yönünden yaklaşılırsa, o zaman görüntüler de çarpımın karmaşık sayılar çarpımı olduğu f '(zo) r çarpımı yönünden f(zo) noktasına yaklaşır.
Türevliliğin bu tip tanımı gerçel türevlilik ile belli başlı ortak özellikler taşımaktadır:
* Her iki türev de doğrusaldır (lineerdir).
* Her iki türev de türevdeki çarpma, bölme ve zincir kuralını sağlarlar.
f fonksiyonu U kümesi içindeki her zo noktasında holomorfik ise, f fonksiyonu U üzerinde holomorfiktir denilir. f fonksiyonu zo etrafındaki bir komşuluk içinde holomorfik ise zo noktasında holomorfiktir denilir. Açık olmayan bir A kümesinde f 'ye holomorfik diyebilmek için ise f 'nin A kümesini de içeren bir açık küme üzerinde holomorfik olması gerekmektedir.
Gerçel türevlilik ve karmaşık türevlilik arasındaki ilişki ise şudur: Eğer f(x + iy) = u(x, y) + iv(x, y) karmaşık fonksiyonu holomorfikse, o zaman u ve v 'nin x ve y 'ye göre birinci kısmi türevleri vardır ve Cauchy-Riemann denklemleri olarak bilinen aşağıdaki ifadeyi sağlarlar:
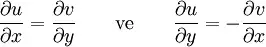
Ancak bu ifadenin tersi her zaman doğru değildir. Doğru olan daha basit bir ters ifade ise şudur: u ve v 'nin sürekli birinci kısmi türevleri varsa ve u ve v Cauchy-Riemann denklemlerini sağlıyorsa, o zaman f holomorfiktir.
Terminoloji
"Holomorfik" kelimesi ilk kez Cauchy'nin öğrencileri olan Briot (1817 - 1882) ve Bouquet (1819 - 1895) tarafından literatüre sokulmuştur ve Yunanca "tam" anlamına gelen őλoς (holos) ve "form","şekil" veya "görünüm" anlamlarına gelen μoρφń (morphe) kelimelerinden oluşur.
Günümüzde birçok matematikçi analitik fonksiyonun daha genel bir kavram olmasından dolayı holomorfik fonksiyon kavramını kullanmayı tercih etmektedir. Bunun bir diğer nedeni ise karmaşık analizde her holomorfik fonksiyonun karmaşık analitik olması gerektiğini ifade eden önemli bir sonuçtur. Ancak yine de, "analitik" terimi daha geniş anlamda kullanılmaktadır.
Özellikler
Karmaşık türevin doğrusal olması ve çarpma, bölme ve zincir kuralına uyması sebebiyle, holomorfik fonksiyonların toplamları, çarpımları ve bileşkeleri yine holomorfiktir ve paydanın sıfır olmadığı yerlerde ise iki holomorfik fonksiyonun bölümleri yine holomorfiktir.
Eğer C, R2 olarak tanımlanırsa, o zaman holomorfik fonksiyonlar, sürekli birinci türevi olan iki gerçel değişkenli ve iki denklemden oluşan kısmi türevsel denklemler kümesi olan Cauchy-Riemann denklemlerini çözen fonksiyonlara denk gelir.
Bütün holomorfik fonksiyonlar gerçel ve sanal kısımlarına ayrılabilirler ve her bir kısım R2 üzerinde Laplace denklemi'nin bir çözümüdür. Başka bir deyişle, holomorfik fonksiyon f(z) 'yi 'u(x, y) + i v(x, y) şeklinde ifade edersek, hem u hem de v harmonik fonksiyonlardır.
Birinci türevin sıfır olmadığı bölgelerde, holomorfik fonksiyonlar açı ve şekil (büyüklük anlamında değil) bağlamında açıkorurdurlar.
Cauchy integral formülü ise bir disk içindeki her holomorfik fonksiyonun, fonksiyonun diskin sınırları üzerindeki değerleriyle belirlendiğini ifade eder.
Her Holomorfik fonksiyon aynı zamanda analiktir. Yani, bir holomorfik fonksiyon f 'nin tanım kümesindeki her a noktasında her mertebeden türevi vardır ve a etrafındaki bir komşulukta fonksiyonun anoktasındaki kendi Taylor serisi'ne denk gelir. Aslında, f fonksiyonu, a 'yı merkez alan ve f 'nin tanım kümesi içinde kalan her disk üzerinde kendi Taylor serisine denk gelir.
Cebirsel bakış açısıyla, açık bir küme üzerindeki holomorfik fonksiyonlar kümesi değişmeli halkadır ve karmaşık vektör uzayıdır. Aslında, bu küme, yarı normun tıkız altkümeler üzerindeki supremumların olduğu bir yerel dışbükey topolojik vektör uzayıdır.
Örnekler
Karmaşık değişkenli ve karmaşık katsayılı bütün polinomlar, sinüs, kosinüs ve üstel fonksiyonlar C üzerinde holomorfiktir. (Aslında trigonometrik fonksiyonlar üstel fonksiyonla ilişkilidir ve Euler formülü yardımıyla tanımlanabilirler).
Karmaşık logaritma'nın ana dallanması C \ {z ∈ R : z ≤ 0} kümesi üzerinde holomorfiktir. Karekök fonksiyonu
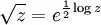
ifadesiyle tanımlanabilir ve bu yüzden log(z) 'nin holomorfik olduğu her yerde holomorfiktir. 1/z fonksiyonu ise {z : z ≠ 0} üzerinde holomorfiktir.
Holomorfik olmayan sürekli fonksiyonların tipik örnekleri ise karmaşık eşlenikler ve gerçel kısımlardır.
Çok Değişkenliler
Çok karmaşık değişkenli karmaşık bir analitik fonksiyon, değişkenlerin yakınsak kuvvet serileri bağlamında yerel olarak genişletilebilirse (disklerin kartezyen çarpımı olan bir polidisk içinde) analitik veya holomorfik olur. Bu koşul Cauchy-Riemann denklemlerinden daha güçlü bir koşuldur ve aşağıdaki gibi ifade edilebilir:
Çok karmaşık değişkenli bir fonksiyonun holomorfik olması ancak ve ancak Cauchy-Riemann denklemlerini sağlamasıyla ve yerel olarak kare-integrallenebilmesiyle gerçekleşir.
Fonksiyonel Analize Ggenişleme
Holomorfik fonksiyon kavramı fonksiyonel analizdeki sonsuz boyutlu uzaylara genişletilebilir. Örneğin, karmaşık sayılar cismi üzerindeki bir Banach Uzayı'nda holomorfik fonksiyon fikri Fréchet ve Gâteaux türevi sayesinde gerçekleştirelebilir.
Holomorfik fonksiyonlar karmaşık analizin temel çalışma araçlarından biridir. Bu fonksiyonlar karmaşık düzlemin yani C'nin açık bir altkümesinde tanımlı, bu altkümedeki her noktada karmaşık anlamda türevli ve aldığı değerler yine C içinde olan fonksiyonlardır. Bu koşul normal gerçel türevlilikten daha güçlüdür. Daha derin anlamda, holomorfik fonksiyon sonsuz kere türevlenebilir ve Taylor serisi ile tanımlanabilir. Her ne kadar daha geniş anlamda (gerçel, karmaşık veya daha genel bir çerçevede) fonksiyonun tanım kümesi içindeki her noktanın komşuluğunda fonksiyonun Taylor serisine eşit olması anlamına gelse de, analitik fonksiyon teriminin holomorfik fonksiyon terimi yerine de kullanıldığı bolca yer vardır. Analitik fonksiyonlar sınıfının karmaşık analizde holomorfik fonksiyonlar sınıfı ile aynı olması karmaşık analizde önemli bir teoremdir. Holomorfik fonksiyonlara bazen kümesine ait bir düzenli fonksiyonlar dendiği de olmaktadır. Karmaşık düzlemin tümünde holomorfik olan fonksiyona tam fonksiyon adı verilir. "a noktasında holomorfik olma" terimi a noktasında türevli manasına gelmekle beraber aynı zamanda karmaşık düzlemde a noktası etrafındaki belli bir açık disk içindeki her noktada türevli anlamına da gelmektedir.
Tanım
U kümesi C 'nin açık bir kümesiyse, f : U → C, U üzerinde tanımlı karmaşık bir fonksiyonsa ve Uzo noktasındaki
limiti varsa, f 'ye z0 noktasında karmaşık türevli denilir. Burada limit z0 noktasına yaklaşan karmaşık sayıların tüm dizileri üzerinden alınır ve bu tür tüm diziler için farkların oranı tek bir sayıya yaklaşmak zorundadır ki o sayı da f '(zo) 'dır. Sezgisel olarak, f fonksiyonu zo 'da karmaşık türevliyse ve zo 'a r yönünden yaklaşılırsa, o zaman görüntüler de çarpımın karmaşık sayılar çarpımı olduğu f '(zo) r çarpımı yönünden f(zo) noktasına yaklaşır.
Türevliliğin bu tip tanımı gerçel türevlilik ile belli başlı ortak özellikler taşımaktadır:
* Her iki türev de doğrusaldır (lineerdir).
* Her iki türev de türevdeki çarpma, bölme ve zincir kuralını sağlarlar.
f fonksiyonu U kümesi içindeki her zo noktasında holomorfik ise, f fonksiyonu U üzerinde holomorfiktir denilir. f fonksiyonu zo etrafındaki bir komşuluk içinde holomorfik ise zo noktasında holomorfiktir denilir. Açık olmayan bir A kümesinde f 'ye holomorfik diyebilmek için ise f 'nin A kümesini de içeren bir açık küme üzerinde holomorfik olması gerekmektedir.
Gerçel türevlilik ve karmaşık türevlilik arasındaki ilişki ise şudur: Eğer f(x + iy) = u(x, y) + iv(x, y) karmaşık fonksiyonu holomorfikse, o zaman u ve v 'nin x ve y 'ye göre birinci kısmi türevleri vardır ve Cauchy-Riemann denklemleri olarak bilinen aşağıdaki ifadeyi sağlarlar:
Ancak bu ifadenin tersi her zaman doğru değildir. Doğru olan daha basit bir ters ifade ise şudur: u ve v 'nin sürekli birinci kısmi türevleri varsa ve u ve v Cauchy-Riemann denklemlerini sağlıyorsa, o zaman f holomorfiktir.
Terminoloji
"Holomorfik" kelimesi ilk kez Cauchy'nin öğrencileri olan Briot (1817 - 1882) ve Bouquet (1819 - 1895) tarafından literatüre sokulmuştur ve Yunanca "tam" anlamına gelen őλoς (holos) ve "form","şekil" veya "görünüm" anlamlarına gelen μoρφń (morphe) kelimelerinden oluşur.
Günümüzde birçok matematikçi analitik fonksiyonun daha genel bir kavram olmasından dolayı holomorfik fonksiyon kavramını kullanmayı tercih etmektedir. Bunun bir diğer nedeni ise karmaşık analizde her holomorfik fonksiyonun karmaşık analitik olması gerektiğini ifade eden önemli bir sonuçtur. Ancak yine de, "analitik" terimi daha geniş anlamda kullanılmaktadır.
Özellikler
Karmaşık türevin doğrusal olması ve çarpma, bölme ve zincir kuralına uyması sebebiyle, holomorfik fonksiyonların toplamları, çarpımları ve bileşkeleri yine holomorfiktir ve paydanın sıfır olmadığı yerlerde ise iki holomorfik fonksiyonun bölümleri yine holomorfiktir.
Eğer C, R2 olarak tanımlanırsa, o zaman holomorfik fonksiyonlar, sürekli birinci türevi olan iki gerçel değişkenli ve iki denklemden oluşan kısmi türevsel denklemler kümesi olan Cauchy-Riemann denklemlerini çözen fonksiyonlara denk gelir.
Bütün holomorfik fonksiyonlar gerçel ve sanal kısımlarına ayrılabilirler ve her bir kısım R2 üzerinde Laplace denklemi'nin bir çözümüdür. Başka bir deyişle, holomorfik fonksiyon f(z) 'yi 'u(x, y) + i v(x, y) şeklinde ifade edersek, hem u hem de v harmonik fonksiyonlardır.
Birinci türevin sıfır olmadığı bölgelerde, holomorfik fonksiyonlar açı ve şekil (büyüklük anlamında değil) bağlamında açıkorurdurlar.
Cauchy integral formülü ise bir disk içindeki her holomorfik fonksiyonun, fonksiyonun diskin sınırları üzerindeki değerleriyle belirlendiğini ifade eder.
Her Holomorfik fonksiyon aynı zamanda analiktir. Yani, bir holomorfik fonksiyon f 'nin tanım kümesindeki her a noktasında her mertebeden türevi vardır ve a etrafındaki bir komşulukta fonksiyonun anoktasındaki kendi Taylor serisi'ne denk gelir. Aslında, f fonksiyonu, a 'yı merkez alan ve f 'nin tanım kümesi içinde kalan her disk üzerinde kendi Taylor serisine denk gelir.
Cebirsel bakış açısıyla, açık bir küme üzerindeki holomorfik fonksiyonlar kümesi değişmeli halkadır ve karmaşık vektör uzayıdır. Aslında, bu küme, yarı normun tıkız altkümeler üzerindeki supremumların olduğu bir yerel dışbükey topolojik vektör uzayıdır.
Örnekler
Karmaşık değişkenli ve karmaşık katsayılı bütün polinomlar, sinüs, kosinüs ve üstel fonksiyonlar C üzerinde holomorfiktir. (Aslında trigonometrik fonksiyonlar üstel fonksiyonla ilişkilidir ve Euler formülü yardımıyla tanımlanabilirler).
Karmaşık logaritma'nın ana dallanması C \ {z ∈ R : z ≤ 0} kümesi üzerinde holomorfiktir. Karekök fonksiyonu
ifadesiyle tanımlanabilir ve bu yüzden log(z) 'nin holomorfik olduğu her yerde holomorfiktir. 1/z fonksiyonu ise {z : z ≠ 0} üzerinde holomorfiktir.
Holomorfik olmayan sürekli fonksiyonların tipik örnekleri ise karmaşık eşlenikler ve gerçel kısımlardır.
Çok Değişkenliler
Çok karmaşık değişkenli karmaşık bir analitik fonksiyon, değişkenlerin yakınsak kuvvet serileri bağlamında yerel olarak genişletilebilirse (disklerin kartezyen çarpımı olan bir polidisk içinde) analitik veya holomorfik olur. Bu koşul Cauchy-Riemann denklemlerinden daha güçlü bir koşuldur ve aşağıdaki gibi ifade edilebilir:
Çok karmaşık değişkenli bir fonksiyonun holomorfik olması ancak ve ancak Cauchy-Riemann denklemlerini sağlamasıyla ve yerel olarak kare-integrallenebilmesiyle gerçekleşir.
Fonksiyonel Analize Ggenişleme
Holomorfik fonksiyon kavramı fonksiyonel analizdeki sonsuz boyutlu uzaylara genişletilebilir. Örneğin, karmaşık sayılar cismi üzerindeki bir Banach Uzayı'nda holomorfik fonksiyon fikri Fréchet ve Gâteaux türevi sayesinde gerçekleştirelebilir.