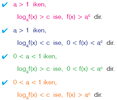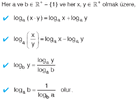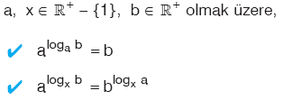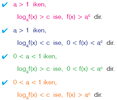Logaritma Konu Anlatımı

I. ÜSTEL FONKSİYONLAR VE LOGARİTMİK FONKSİYONLAR​

2y = 24 eşitliğini sağlayan y değerini bulmak için yapılan işleme üslü denklemi çözme denir. (y = 4)

Buraya kadar anlatılan bilgiler 6a = 10 eşitliğini sağlayan a değerini bulmak için yeterli değildir. Bu eşitliği sağlayan a değerini bulmak için yapılan işleme logaritma alma denir.

A. ÜSTEL FONKSİYONLAR​

olmak üzere,



biçiminde tanımlanan fonksiyona üstel fonksiyon adı verilir.

a > 0 olduğundan f(x) = ax > 0 olur.

B. LOGARİTMA FONKSİYONU​

olmak üzere,



biçiminde tanımlanan üstel fonksiyonun ters fonksiyonuna logaritma fonksiyonu denir.


şeklinde gösterilir. Buna göre,


y = logₐx ifadesinde y ∈ R sayısına x ∈ R⁺ sayısının a tabanına göre logaritması denir ve ‘‘y eşittir a tabanına göre logaritma x ’’ şeklinde okunur.

C. LOGARİTMA FONKSİYONUNUN ÖZELLİKLERİ​

Kural
1 den farklı her a pozitif reel sayısının a tabanına göre logaritması 1 dir. Buna göre, her a ∈ R+ – {1} olmak üzere logₐa= 1 dir.

Kural
Her tabana göre, 1 in logaritması 0 dır. Buna göre, her a ∈ R⁺– {1} olmak üzere logₐ₁= 0 dır.
Kural


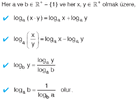Kural



Kural


Kural

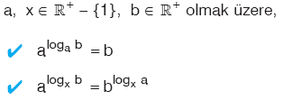
D. ONLUK LOGARİTMA FONKSİYONU​

f(x) = logₐx fonksiyonunda taban a = 10 alınırsa f(x) fonksiyonuna onluk logaritma fonksiyonu denir ve kısaca logx biçiminde gösterilir.

f: R⁺ → R, f(x)=log₁₀x= logx

1 den büyük sayıların on tabanına göre logaritması pozitiftir.

1 den küçük pozitif sayıların on tabanına göre logaritması negatiftir.

Not: Logaritmanın tabanı yazılmamışsa tabanı 10 demektir.

Kural
x > 1 olmak üzere, x in onluk logaritmasının tam kısmı, x in basamak sayısının bir eksiğine eşittir. 0 < y < 1 olmak üzere, y nin ondalık kesir biçiminde yazılışında, sıfırdan farklı ilk rakamın solundaki sıfır sayısı K ise, logy nin eşitinin tam kısmı –(K – 1) dir.

DOĞAL LOGARİTMA FONKSİYONU​

f(x) = logₐx fonksiyonunda taban

ℓ = 2,718281828459045235360287471352… alınırsa (ℓ sayısı irrasyonel bir sayı olup yaklaşık değeri 2,718 kabul edilir.) doğal logaritma fonksiyonu elde edilir. Doğal logaritma fonksiyonu kısaca lnx biçiminde gösterilir. Bu durumda,

f: R⁺ → R, f(x)=logₑx= lnx tir.

İşlemlerde genellikle logex yerine lnx ifadesi kullanılır.

Logaritma Fonksiyonun Tersinin Alınması​

1. Fonksiyon y’e eşitlenir.
2. x yalnız bırakılır.
3. x yerine f⁻¹(x) yazılır, y yerine x yazılır.

LOGARİTMALI DENKLEMLER​

Özellik
a sayısı 1 sayısından farklı bir pozitif sayı olmak üzere, tabanı a olan logaritmalı denklem, logₐf(x) = b ise f(x) = aᵇ dir. logₐf(x) =logₐg(x) ise f(x) = g(x) dir.

Logaritmalı denklemleri bu özellikleri kullanarak çözeriz.

Logaritmanın tanımından, f(x) > 0 ve g(x) > 0 olmalıdır.

LOGARİTMALI EŞİTSİZLİKLER​

Kural
logₐf(x) in işareti a ya bağlı olduğundan eşitsizlik çözümlerinde aşağıdaki bilgileri kullanırız.

Logaritmanın, üslü denklemlerin tersi olduğunu doğru bir şekilde belirtmişsiniz. Üslü denklemlerden farklı olarak, logaritma işlemi genellikle daha karmaşık denklemleri çözmek için kullanılır. Üstel fonksiyonlar ve logaritmik fonksiyonlar matematikte önemli bir yer tutar ve birbirlerini tamamlayan konseptlerdir. Üstel fonksiyonlar, genellikle x'in üssü şeklinde ifade edilen fonksiyonlardır, logaritmik fonksiyonlar ise bu fonksiyonların tersidir ve belirli bir tabana göre x'in logaritması olarak ifade edilir. Bu konuların matematikteki uygulama alanları oldukça geniştir ve özellikle bilim ve mühendislik alanlarında sıkça karşımıza çıkarlar.