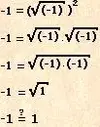Doğru Parçası Paradoksu:
Önce doğru parçasının tarifini yapalım:
Doğru Parçası: Başlangıcı ve sonu olan ve sonsuz adet noktadan oluşan doğru. Pekiyi nokta nedir?
Nokta: Kalemin kağıda bıraktığı en küçük iz veya belirti.Malûmdur ki noktanın boyutu yoktur. O halde dikkat. Paradoks başlıyor:
Noktanın boyutu olmadığına göre iki noktanın yan yana gelmesi bir şey ifade etmez. 100 nokta veya 1 milyar nokta da yan yana geldiğinde herhangi bir şekil oluşturmaz.( Çünkü şekil oluşturması için gerekli olan boyut özelliğini sağlamıyor) Bu şuna benzer ki; sıfır ile sıfırın toplamı yine sıfırdır. Milyarlarca sıfırı toplasak 'yarım' dahi etmez. O halde doğrunun tanımında bir hata var. Çünkü sonsuz adet noktanın yan yana gelmesi bir şey ifade etmez! Noktanın çok çok az da olsa boyutu olduğunu kabul etmemiz gerekir. Bu sefer de noktanın tarifi hatalı olur.
Noktayı boyutlu kabul edelim. Karşımıza bir paradoks daha çıkar; doğru parçasında sonsuz adet nokta olduğuna göre doğru parçasının da uzunluğu sonsuz olmalıdır. Çünkü çok az da olsa boyutu olan bir şeyden sonsuz adedi yanyana gelirse sonsuz uzunluk olur.
2+2=5 ¿?
X = Y ................................................ol sun
X² = X.Y............................................eşitli ğin her iki tarafını 'X' ile çarptık.
X² - Y² = XY - Y²..............................her iki taraftan 'Y²' çıkardık.
(X + Y).(X - Y) = Y.( X-Y )...............sol tarafı çarpanlara ayırdık, sağ tarafı 'Y' parantezine aldık.
( X + Y ) = Y.....................................( X - Y )'ler sadeleşti.
X + X = X..........................................X = Y olduğundan,
2.X = X..............................................'X' leri topladık.
2 = 1 ................................................'X' ler sadeleşti.
3 + 2 = 1 + 3....................................her iki tarafa '3' ilâve ettik.
5 = 4.................................................. buradan,
5 = 2 + 2.......................................'4'ü, '2+2' şeklinde yazdık. HATA NEREDE?
Önce doğru parçasının tarifini yapalım:
Doğru Parçası: Başlangıcı ve sonu olan ve sonsuz adet noktadan oluşan doğru. Pekiyi nokta nedir?
Nokta: Kalemin kağıda bıraktığı en küçük iz veya belirti.Malûmdur ki noktanın boyutu yoktur. O halde dikkat. Paradoks başlıyor:
Noktanın boyutu olmadığına göre iki noktanın yan yana gelmesi bir şey ifade etmez. 100 nokta veya 1 milyar nokta da yan yana geldiğinde herhangi bir şekil oluşturmaz.( Çünkü şekil oluşturması için gerekli olan boyut özelliğini sağlamıyor) Bu şuna benzer ki; sıfır ile sıfırın toplamı yine sıfırdır. Milyarlarca sıfırı toplasak 'yarım' dahi etmez. O halde doğrunun tanımında bir hata var. Çünkü sonsuz adet noktanın yan yana gelmesi bir şey ifade etmez! Noktanın çok çok az da olsa boyutu olduğunu kabul etmemiz gerekir. Bu sefer de noktanın tarifi hatalı olur.
Noktayı boyutlu kabul edelim. Karşımıza bir paradoks daha çıkar; doğru parçasında sonsuz adet nokta olduğuna göre doğru parçasının da uzunluğu sonsuz olmalıdır. Çünkü çok az da olsa boyutu olan bir şeyden sonsuz adedi yanyana gelirse sonsuz uzunluk olur.
2+2=5 ¿?
X = Y ................................................ol sun
X² = X.Y............................................eşitli ğin her iki tarafını 'X' ile çarptık.
X² - Y² = XY - Y²..............................her iki taraftan 'Y²' çıkardık.
(X + Y).(X - Y) = Y.( X-Y )...............sol tarafı çarpanlara ayırdık, sağ tarafı 'Y' parantezine aldık.
( X + Y ) = Y.....................................( X - Y )'ler sadeleşti.
X + X = X..........................................X = Y olduğundan,
2.X = X..............................................'X' leri topladık.
2 = 1 ................................................'X' ler sadeleşti.
3 + 2 = 1 + 3....................................her iki tarafa '3' ilâve ettik.
5 = 4.................................................. buradan,
5 = 2 + 2.......................................'4'ü, '2+2' şeklinde yazdık. HATA NEREDE?