Günlük dilde “limit” kelimesi bir miktar, bir fikir ya da herhangi bir şeyin ötesine geçemeyeceği sınırları tanımlamak için kullanılır. Örneğin, hız sınırı size yasal olarak izin verilen maksimum hızı ve kredi kartı limitiniz kullanabileceğiniz maksimum bakiyeyi bildirir. Bu iki örnek de üst sınırları temsil etmektedir. Limit, elbette alt sınırlar için de geçerlidir. Mesela, bir kredi almak için gerekli minimum kredi puanı.
Matematikte, limit kavramı bir açıdan yukarıdaki örneklerle benzer fakat tam olarak aynı diyemeyiz. Limit, bir sınıra gittikçe yakınlaştığımızda ne olduğu hakkında konuşmak için kullanıldığında aynıdır. Fakat, minimum veya maksimum değerlerle ilgili olmak zorunda olmadığı için de farklıdır. Bunun yerine, matematikte limit fikri ve ele alınan sınırların türü çok daha soyut olabilir.
Peki matematikte limit nasıl çalışır? Ve neden önemlidir? Keşfetmek üzereyiz.
Bir Daireyi Nasıl Tanımlarsınız?
Limitin matematiksel tanımını anlamak için dairenin matematiksel tanımı hakkında biraz konuşalım. Özellikle de daire ile kastettiğimiz şeyi tam olarak tanımlayabileceğimiz çeşitli yollar hakkında. İlki geometrik olarak, daire; üzerindeki bütün noktaların merkezdeki noktaya uzaklığı aynı olan iki boyutlu (kâğıt düzleminde) bir eğridir. Ve daireyi tanımlamanın bir de cebirsel bir yolu var. x2+y2=r2 denkleminin çözümüne ait olan xy düzlemindeki bütün noktaların oluşturduğu şekle daire denir (r=yarıçap). Elbette, bu iki tanım birbiriyle ilişkilidir – aslında, aynı şeyi söyleyen iki farklı yoldurlar.
Bunların her ikisi de bir daireyi tanımlamanın ince ve şık yolları olmakla birlikte, daha ilginç olan bir yol var.
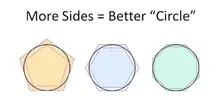
İşte bu şekilde; Eşkenar üçgen çizerek (veya çizimi hayal ederek) başlayın, bu üçgenin yanına bir kare çizin. Dizideki bir sonraki aşamada bir düzgün beşgen çizin, daha sonra düzgün altıgen, düzgün yedigen ve bu şekilde devam edin. Daha fazla kenarlı düzgün çokgenler çizdikçe şekillere bir şey olduğunu fark ettiniz mi? Bir şeylere benzemeye başladığını fark ettiniz mi? Belki bir daire?
Matematikte Limit Ne Anlama Gelir?
Eğer düşünürseniz, sistematik bir şekilde bir öncekinden bir tane daha fazla kenara sahip düzgün çokgenler çizme prosedürüne süresiz bir şekilde devam edebileceğimizi göreceksiniz. Bunu yapmak için yeterince sabrınız ya da daha da önemlisi zamanınız olmadığı için yedinci şekilde duruyoruz. Ancak sonsuza kadar devam etme gerçeği önemlidir. Aslında bu durum limit kavramını matematiksel olarak anlamak için anahtardır.
Düzgün çokgenimizdeki kenar sayısını artırdığımızda çizdiğimiz şekil giderek daha da daire şeklinde gözükmeye başlar. Yedi kenarlıda durduk fakat 10 kenarlı bir düzgün çokgen çizdiğinizi hayal edebilirsiniz ya da 50, 100, 1000, 10000 vs. Kenar sayısı ne kadar çok artarsa şekiller mükemmel bir daireye o kadar çok yaklaşır. Matematik dilinde düzgün çokgenin kenar sayısının limiti sonsuza gittiğinde çizdiğimiz şekil bir daire olacaktır deriz.
Elbette ki sonsuz sayıda kenarı olan bir düzgün çokgen çizemeyiz ama bu limite gittikçe daha da yakınlaşarak mükemmel bir daire elde etmeye çok daha yakınlaşabiliriz. Eğer bu yolda sonsuza kadar devam ederseniz yavaş yavaş bu limite daha da yakınlaşacaksınız. Bu durumda ulaştığımız limit bir dairedir. Fakat limit kavramı geometrik şekillerle sınırlı değildir.
Limit ve Diziler
Aslında matematikte limit kavramı çok daha genel bir fikirdir. Örnek olarak 1/2n ifadesinde n’ e gittikçe artan tam sayılar verdiğimizde oluşan sayılar dizisini alalım. Diğer bir deyişle n=1, n=2, n=3, n=4 … olduğunda ifadenin alacağı değerleri inceleyelim. Kısa bir hesaplama ile dizimizdeki sayıların 1/2, 1/4, 1/8, 1/16 … şeklinde olacağını görürüz.
Buradaki soru; n’ in çok daha büyük değerlerinde bunu yapmaya devam ederseniz dizi hangi sayıya yaklaşacaktır? Diğer bir deyişle n sonsuza giderken dizi asla ulaşamasa bile hangi sayıya yaklaşacak? Bu durumda cevabın görülmesi oldukça kolay: n arttıkça dizideki sayıların değeri gittikçe küçülür. n’ in sonsuz büyüklükteki değerlerinin limitinde dizi sıfıra yaklaşır. Hiçbir zaman sıfıra ulaşmaz, ama istediğiniz kadar yaklaşır.
Gördüğünüz gibi buradaki limit fikri bir önceki geometrik örneğimizden oldukça farklı duruyor. Fakat farklı görünseler bile ikisinin de kalbinde sınırlara yaklaşma konusunda aynı soyut fikir yatıyor.
Matematikte, limit kavramı bir açıdan yukarıdaki örneklerle benzer fakat tam olarak aynı diyemeyiz. Limit, bir sınıra gittikçe yakınlaştığımızda ne olduğu hakkında konuşmak için kullanıldığında aynıdır. Fakat, minimum veya maksimum değerlerle ilgili olmak zorunda olmadığı için de farklıdır. Bunun yerine, matematikte limit fikri ve ele alınan sınırların türü çok daha soyut olabilir.
Peki matematikte limit nasıl çalışır? Ve neden önemlidir? Keşfetmek üzereyiz.
Bir Daireyi Nasıl Tanımlarsınız?
Limitin matematiksel tanımını anlamak için dairenin matematiksel tanımı hakkında biraz konuşalım. Özellikle de daire ile kastettiğimiz şeyi tam olarak tanımlayabileceğimiz çeşitli yollar hakkında. İlki geometrik olarak, daire; üzerindeki bütün noktaların merkezdeki noktaya uzaklığı aynı olan iki boyutlu (kâğıt düzleminde) bir eğridir. Ve daireyi tanımlamanın bir de cebirsel bir yolu var. x2+y2=r2 denkleminin çözümüne ait olan xy düzlemindeki bütün noktaların oluşturduğu şekle daire denir (r=yarıçap). Elbette, bu iki tanım birbiriyle ilişkilidir – aslında, aynı şeyi söyleyen iki farklı yoldurlar.
Bunların her ikisi de bir daireyi tanımlamanın ince ve şık yolları olmakla birlikte, daha ilginç olan bir yol var.
İşte bu şekilde; Eşkenar üçgen çizerek (veya çizimi hayal ederek) başlayın, bu üçgenin yanına bir kare çizin. Dizideki bir sonraki aşamada bir düzgün beşgen çizin, daha sonra düzgün altıgen, düzgün yedigen ve bu şekilde devam edin. Daha fazla kenarlı düzgün çokgenler çizdikçe şekillere bir şey olduğunu fark ettiniz mi? Bir şeylere benzemeye başladığını fark ettiniz mi? Belki bir daire?
Matematikte Limit Ne Anlama Gelir?
Eğer düşünürseniz, sistematik bir şekilde bir öncekinden bir tane daha fazla kenara sahip düzgün çokgenler çizme prosedürüne süresiz bir şekilde devam edebileceğimizi göreceksiniz. Bunu yapmak için yeterince sabrınız ya da daha da önemlisi zamanınız olmadığı için yedinci şekilde duruyoruz. Ancak sonsuza kadar devam etme gerçeği önemlidir. Aslında bu durum limit kavramını matematiksel olarak anlamak için anahtardır.
Düzgün çokgenimizdeki kenar sayısını artırdığımızda çizdiğimiz şekil giderek daha da daire şeklinde gözükmeye başlar. Yedi kenarlıda durduk fakat 10 kenarlı bir düzgün çokgen çizdiğinizi hayal edebilirsiniz ya da 50, 100, 1000, 10000 vs. Kenar sayısı ne kadar çok artarsa şekiller mükemmel bir daireye o kadar çok yaklaşır. Matematik dilinde düzgün çokgenin kenar sayısının limiti sonsuza gittiğinde çizdiğimiz şekil bir daire olacaktır deriz.
Elbette ki sonsuz sayıda kenarı olan bir düzgün çokgen çizemeyiz ama bu limite gittikçe daha da yakınlaşarak mükemmel bir daire elde etmeye çok daha yakınlaşabiliriz. Eğer bu yolda sonsuza kadar devam ederseniz yavaş yavaş bu limite daha da yakınlaşacaksınız. Bu durumda ulaştığımız limit bir dairedir. Fakat limit kavramı geometrik şekillerle sınırlı değildir.
Limit ve Diziler
Aslında matematikte limit kavramı çok daha genel bir fikirdir. Örnek olarak 1/2n ifadesinde n’ e gittikçe artan tam sayılar verdiğimizde oluşan sayılar dizisini alalım. Diğer bir deyişle n=1, n=2, n=3, n=4 … olduğunda ifadenin alacağı değerleri inceleyelim. Kısa bir hesaplama ile dizimizdeki sayıların 1/2, 1/4, 1/8, 1/16 … şeklinde olacağını görürüz.
Buradaki soru; n’ in çok daha büyük değerlerinde bunu yapmaya devam ederseniz dizi hangi sayıya yaklaşacaktır? Diğer bir deyişle n sonsuza giderken dizi asla ulaşamasa bile hangi sayıya yaklaşacak? Bu durumda cevabın görülmesi oldukça kolay: n arttıkça dizideki sayıların değeri gittikçe küçülür. n’ in sonsuz büyüklükteki değerlerinin limitinde dizi sıfıra yaklaşır. Hiçbir zaman sıfıra ulaşmaz, ama istediğiniz kadar yaklaşır.
Gördüğünüz gibi buradaki limit fikri bir önceki geometrik örneğimizden oldukça farklı duruyor. Fakat farklı görünseler bile ikisinin de kalbinde sınırlara yaklaşma konusunda aynı soyut fikir yatıyor.