Piramit, Koni ve Kürenin Hakkında; Özellikleri, Alanı ve Hacim Hesabı Formülü

KÜRE​

Uzayda bir noktadan eşit uzaklıktaki noktaların geometrik yerine küre yüzeyi denir. Küre yüzeyinin sınırladığı cisme küre adı verilir. Sabit noktaya kürenin merkezi, merkezin küre yüzeyine uzaklığına da kürenin yarıçapı denir.



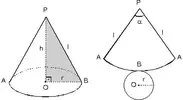
O merkezli R yarıçaplı kürede;

KÜRE HACİM FORMÜLÜ


Yüzey alanı

Yüzey alanı:

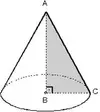
1. Küre Dilimi​

[KL] çap

m(AOB) = α

şekildeki gibi kesilip çıkarılan küre diliminin hacmi

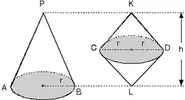
2. Küre Kapağı​

Bir küre merkezinden |OP| uzaklıkta bir düzlemle kesildiğinde kesit alanının daire şeklinde olduğu görülür.

Kesilip çıkarılan kısma küre kapağı denir. Kesitin merkezinden uzaklığına |OP|, kesitin yarıçapına r ve kürenin yarıçapına R dersek

|OP|² + r² = R² eşitliği vardır. h = R - |OP|

Küre kapağının alanı= 2πRh

Yandaki şekildeki gibi olan

Küre parçasının hacmi:

Düzgün Sekizyüzlü​

Bütün ayrıtları birbirine eş ve yüzeyleri sekiz eşkenar üçgenden oluşan cisme düzgün sekizyüzlü denir.
Bir ayrıtına a dersek yan yüz yüksekliği: olur.

Piramidin hacmi olduğundan;



Yüzey şekilleri eşkenar üçgen olduğundan

Düzgün Altıgen Piramit​

Tabanı düzgün altıgen olan piramide düzgün altıgen piramit denir.


Yan yüzeyleri altı adet eş ikizkenar üçgenden oluşur.

Düzgün Altıgen Piramidin Alanı 1 tane altıgen ve 6 tane ikizkenar üçgenin alanları toplamından oluşur?

Düzgün altıgenin alanı:

KONİ​

Koni, matematikte, bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekildir.

Tabanı daire biçiminde olan piramide koni adı verilir.


Taban alanı = olduğundan



bulunur. Yan yüzeyleri altı adet eş ikizkenar üçgen oluşur.

KONİ​

Tabanı daire biçiminde olan piramite koni adı verilir.

Burada;

Taban yarıçapı |OB| = r
Cisim yüksekliği |PO| = h olur.
|PA| = |PB| = l uzunluğuna ana doğru denir.
POB dik üçgeninde,
h² + r² = l² bağıntısı vardır.
Koninin yanal alanı bir daire dilimidir.

Daire diliminin alanı, yay uzunluğu ile yarıçapın çarpımının yarısıdır. Yay uzunluğu taban çevresine eşit olduğundan,

Yanal alan= pr2+prl
Tüm alan bulunurken, taban alanı da ilave edilir.

Tüm alan = šr2 + šrl

Daire diliminin merkez açısına a dersek oranı elde ederiz.

Yükseklikleri ve taban yarıçapları eşit olan iki cismin hacimleri de birbirine eşittir.




Üçgensel şekiller bir kenarı etrafında döndürüldüğünde koni elde edilir. Şekildeki ABC dik üçgeninin AB kenarı etrafında döndürülmesi ile |BC| yarıçaplı ve yüksekliği |AB| olan koni elde edilir.



Kesik piramitlerin hacimleri bulunurken cisim piramide tamamlanır.

[O₁B] // [O₂D] olduğundan
benzerliği vardır.

Küçük koninin büyük koniye benzerlik oranı dir.
Alanları oranı benzerlik oranının karesi olduğundan, alanlar oranı olur.

Hacimler oranı ise benzerlik oranının küpüdür. r₁ yarıçaplı küçük koninin hacmine V₁, r₂ yarıçaplı büyük koninin hacmine V₂ dersek

PİRAMİTLER​

Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir.



T noktası piramidin tepe noktasıdır. Kapalı bölge ise piramidin tabanıdır. Piramit; tabanı oluşturan şeklin ismiyle adlandırılır. Taban kare ise, kare piramit; taban altıgense altıgen piramit gibi.

Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.

T noktasının taban düzlemi üzerindeki dik izdüşümüne H dersek [TH] piramidin yüksekliği olur.

|TH| = h biçiminde yazılır. [TA], [TB], [TC]… piramidin yanal ayrıtlarıdır.

Piramitlerin hacmi taban alanı ile yüksekliğin çarpımının üçte biri kadardır.





1.Kare Piramit (Tabanı kare olup yan yüzleri eşkenar üçgen olan piramit)


Kare piramidin tabanı kare biçimindedir. Yan yüzeyleri ise dört adet ikizkenar üçgenden oluşur.

İkizkenar üçgenlerin taban uzunlukları piramidin tabanının bir kenarına eşittir.

|PH| = h piramidin yüksekliğidir.

Yan yüz yüksekliği |PK| dır.
Tabanının bir kenarına a dersek

Buradan yan yüz yüksekliği |PK|² = h² + ()² olur.




Tüm alan yan yüz alanları ile taban alanının toplamına eşittir.

2. Eşkenar Üçgen Piramit

Tabanı eşkenar üçgen olan piramitlere eşkenar üçgen piramit denir.


veya

3. Düzgün Dörtyüzlü​

Dört yüzü de eşkenar üçgenlerden oluşan cisimdir. Yükseklik, tabanı oluşturan üçgenin ağırlık merkezine iner.

Düzgün dörtyüzlünün bütün kenar uzunlukları birbirlerine eşittir.

Düzgün dörtyüzlü bir düzgün üçgen piramittir. Çünkü tabanı eşkenar üçgendir ve yükseklik, tabanı, eşkenar üçgenin merkezinde keser.

Bir ayrıtı a olan düzgün dörtyüzlünün;


Bir düzgün dörtyüzlünün kenar uzunluğu a olmak üzere: