Tam Sayının Tanımı
Tam sayılar doğal sayılar ve sayma sayılarını kapsayan kesirli, köklü ve ondalıklı olarak ifade edilmeyip tam olan sayılara tam sayılar denir. Günlük hayatımızda doğal sayılar ve sayma sayıları alışveriş yapma, borç verme - borç alma, bulunduğunuz konumdan ileri gitme - geri gitme durumlarda ihtiyaçlarımızı karşılamakta verimsiz ve yetersiz kalır.
Bu gibi durumlarda tam sayılara ihtiyaç duyarız. Tam sayılar önlerine aldıkları "+" ve "-" işaretleriyle pozitif ve negatif olarak ifade edilebilerek bu ihtiyacımızı karşılayabilir. Bu özelliğiyle tam sayılar doğal sayılar ve sayma sayılarından farklı olarak yönlü sayı ölma özelliğini barındırır. Yani "+" işareti pozitif yönlü tam sayıları belirtirken "-" işareti negatif yönlü tam sayıları belirtir.
Tam sayılar - ve + işaretleri hariç herhangi başka bir matematik işareti bulundurmazlar. Geriye kalan diğer işareti bulunduran sayılar tam sayı değildir.
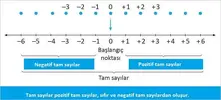
Tam sayılar Z işareti ile gösterilir. - sonsuzdan, + sonsuza kadar giden sayılar kümesidir. Z = {-∞, ... -3, -2, -1, 0, 1, 2, 3 ..., ∞} şeklinde gösterilir.
Pozitif Tam Sayılar
Bir tam sayı önüne "+" işareti alarak pozitif yönlü olarak belirtilen sayılara pozitif tam sayılar denir. Örnekleyecek olursak; alışveriş yaparken toplam paranız, yaptığınız alışveriş maliyetinden fazlaysa arta paranız kalır. Cebinizde kalan paranız arta kaldığı için "+" değere sahip olup pozitiftir. Z
+ = {1, 2, 3, ..., ∞} şeklnde ifade edilir. Aşağıda örnekleri verilmiştir.
2, 13, 37, 141, 313, 8415, 213123, 32423, 65756, 67657, 21412412, 89789788789
Negatif Tam Sayılar
Bir tam sayı önüne "-" işareti alarak negatif yönlü olarak belirtilen sayılara negatif tam sayılar denir. Örnekleyecek olursak; alışveriş yaparken toplam paranız, yaptığınız alışveriş maliyetinden az ise borçlu duruma düşer, bir miktar daha para ödemek zoruda kalırsınız. Kalan borcunuz paranız eksik olduğu için "-" değere sahip olup negatiftir. Z
- = {∞, ..., -3, -2 -1} şeklinde ifade edilir. Aşağıda örnekleri verilmiştir.
-5312341234, -2312312, -45643, -7321, - 6434, -1219, -987, -456, -78, -45, -9, -3
Tam Sayılarda Başlangıç Noktası
Tam sayılar yönlü sayılar olmasına rağmen "+" veya "-" işaretlerinden birini barındırmayarak yönsüz olan bir sayıyı da barındırır. Bu sayı 0'dır. 0 ne pozitif tam sayılar grubuna ne de negatif sayılar grubuna girer. Negatif veya pozitif olmayan bu tam sayı tam sayıların başlangıç noktasını ifade eder.
0 en küçük tam sayı ya da en büyük tam sayı olmamakla birlikte ilk tam sayı veya son tam sayı da değil, tam sayıların tam orta noktasıdır. 0'ın sağındaki sayılar yani aynı zamanda sayma sayıları olarak da adlandırılan sayılar pozitif tam sayılardır.
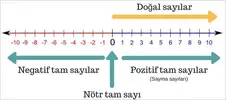
0'ın solunda bulunan sayılar ise negatif tam sayılardır. Tam sayılardan pozitif tam sayıları ve negatif tam sayıları çıkarmamız durumda kalan sayı 0 tam sayısıdır.
Tam Sayılarda İşlemler
Tam sayılardaki işlemler doğal sayılarda yapılan& işlemler ile benzerlik gösterir. Sadece tam sayılar - işareti de alabilirler. Doğal sayılar ile yapılan işlemler 0 ve pozitif tam sayılar ile yapılan işlemler işe ayınıdır. Tam sayılarda matematikte kullanılan 4 işlemin yanısıra negatif sayılar bulunduğu için mutlak değer işlemi de kullanılır.
Tam sayılarda işlem önceliği diğer işlemlerde olduğu gibi sırasıyla mutlak değer- parantez- çarpma - bölme- toplama - çıkarma şeklinde ilerler. Negatif sayılar pozitif sayılar ile toplanırken sayıların mutlak değerleri arasında çıkarma işlemi şeklinde de yapılabilir.
Tam Sayılarda İşlemlerde İşaretler
Tam sayılarda işlemler yapılırken sayılar işaretsiz gibi düşünüp mutlak değerleri ile işlemler yapıldıktan sonra işaretler arasında da işlem yapılıp işaret belirlenebilir. İşaretler arasındaki işlemler aşağıdaki gibidir.
(+) + (+) = (+),
(+) + (-) = (+ veya eksi) (mutlak değeri büyük olanın işaretini alır.),
(-) + (-) = (-),
(-) + (+) = (+ veya eksi) (mutlak değeri büyük olanın işaretini alır.),
(+) x (+) = (+),
(+) x (-) = (-),
(-) x (-) = (+),
(+) ÷ (+) = (+),
(+) ÷ (-) = (-),
(-) ÷ (-) = (+),
(+) - (+) = (+ veya eksi) (çıkarılan sayı büyükse sonuç +, çıkan sayı büyükse sonuç - işaretini alır),
(+) - (-) = (+),
(-) - (-) = (+ veya eksi) (çıkarılan sayı büyükse sonuç +, çıkan sayı büyükse sonuç - işaretini alır),
(-) - (+) = (-)
işaretleri alınır.
Tam Sayılarda Mutlak Değer
Bir tam sayının mutlak değeri o sayının başlangıç noktasına yani 0'a olan uzaklığını belirtir. Tam sayıların 0'a olan uzaklıkları mesafe birimi olduğu için ve mesafeler yönlü ifadeler olmadığı için aradaki uzaklı pozitif olmak zorundadır. Yani sayı negatif de olsa pozitif de olsa sayının 0'a uzaklığı yani mutlak değeri pozitiftir. Aşağıda örnekler mutlak değeri daha iyi anlamanızı sağlar.
|-4| = 4,
|2|= 2,
|-13|=13,
|-154|= 154,
|78|= 78,
|191| =191
Tam Sayılar, Doğal Sayılar, Sayma Sayıları, Rasyonel Sayılar
Tam sayılar rasyonel sayıların alt kümesiyken doğal sayıları kapsar ve doğal sayılar tam sayıların alt kümesiyken sayma sayıları kapsar. Yani;
- Her sayma sayısı bir doğal sayı,
- Her doğal sayı bir tam sayı,
- Her tam sayı aynı zamanda bir rasyonel sayıdır.
Tam Sayılar Hangileridir?
Tam sayılar -∞ ile +∞ arasında bulunan ve tam olan sayılardır. -2112, -764, -97, 0, 34, 118, 6521 tam sayı örnekleridir.
 Alıntıdır...
Alıntıdır...