Matematikte terim testi, ıraksaklık testi veya ıraksaklık için n'inci terim testi bir sonsuz serinin ıraksaklığını belirlemenin basit bir yöntemidir:
*
ise veya limit yok ise, o zaman 
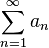ıraksar.
Çoğu yazar bu teste isim vermez veya verirlerse de kısa bir isim verir.
Kullanımı
Daha güçlü yakınsaklık testlerinin aksine, terim testi kendi başına bir serinin yakınsak seri olduğunu ifade etmez. Bilhassa, testin tersi doğru değildir. Bunun yerine
* 
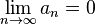ise, o zaman 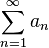yakınsayabilir de yakınsamayabilir de.
denilebilir. Harmonik seri, terimleri 0'a giden ancak ıraksak olan bir serinin klasik bir örneğidir. [3] Harmonik serilerin daha genel bir sınıfı olan p-serileri, yani
testin muhtemel sonuçlarını ortaya çıkaran güzel bir örnektir:
* p ≤ 0 ise, o zaman terim testi serinin yakınsak olduğunu söyler.
* 0 < p ≤ 1 ise, o zaman terim testi sonuçsuzdur; ancak seri integral testi ile ıraksaktır.
* 1 < p ise, o zaman terim testi sonuçsuzdur; ancak seri yine integral testi ile yakınsaktır.
Kanıtlar
Test genelde devrik biçimde kanıtlanır:
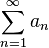*yakınsarsa, o zaman 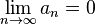olur.
Limit manipülasyonu
sn serini kısmi toplamları ise, o zaman serinin yakınsaması varsayımı, belli bir s için
anlamına gelir. O zaman
olur.
Cauchy ölçütü
Serinin yakınsadığı varsayımı Cauchy yakınsaklık testini sağladığı anlamına gelmektedir: Her
için bir N sayısı vardır öyle ki
ifadesi n > N ve p ≥ 1 için tutar. p = 1 koymak ise tanımın ifadesini, yani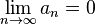ifadesini kurtarır.
Kapsam
Terim testinin en basit çeşiti gerçel sayıların sonsuz serilerine uygulanır. Üstteki iki kanıt, Cauchy ölçütünü veya limitin doğrusallığını kullanarak, diğer herhangi bir normlu vektör uzayında da geçerlidir.
