Yüzey ve Yüzeyin Özellikleri
Yüzey, matematikte ve özellikle topolojide iki boyutlu çokkatlı. İki gerçel değişkenli ve gerçel değerli bir fonksiyonun üç boyutlu uzayda (R³) grafiği tipik yüzey örneğidir. Ayrıca dünya yüzeyi, bir yumurtanın kabuğu, bir simit birer yüzeydir.
Bir yüzeyin 2 boyutlu bir çokkatlı olması, öncelikle onun (belirli özellikleri sağlayan) bir topolojik uzay olması demektir. Bunun yanında yüzeyin verilen (herhangi) bir x noktası çevresinde öyle bir komşuluk bulunabilir ki, bu komşuluk 2 boyutlu uzayın bir parçasına benzer. Bu komşuluğa yama denir. Bu benzeme uyarınca, x çevresinde sağ-sol ve yukarı-aşağı kavramları iyi bir biçimde tanımlanabilir. Daha iyi bir deyişle, x'in çevresine bir koordinat sistemi döşenebilir. Böylece yüzey, bir düzlem parçası olmasa bile x çevresindeki noktalar bir düzlemdeymiş gibi koordinatlara sahip olur.
Dünya yüzeyi matematiksel olarak bir yüzeydir. Dünyanın çizilen her haritası, yukarıdaki anlamda bir koordinat sistemi tarif eder. Bu sayede denizcilikte yön bulma kolaylaşır ve iki denizci aynı koordinat sisteminde konuşarak birbirleriyle anlaşabilir. Dünya yüzeyi için standart koordinat sistemi, enlem ve boylamlarla verilir. Örneğin, dünya yüzeyinden gün dönümü çizgisi ve kutuplar silindiğinde kalan parçaya (180^{\circ} Doğu, 180^{\circ} Batı) ila (90^{\circ} Kuzey, 90^{\circ} Güney) koordinatları verilerek bu parça bir yamaya dönüştürülebilir. Gün dönümü çizgisi ya da kutupların silinmediği durumda bazı enlem-boylam çiftlerinin aynı noktayı tarif edeceklerine dikkat ediniz.
Topolojik bir yüzey, her zaman R³'te görülemeyebilir. Örneğin gerçel izdüşümsel düzlem ya da Klein şişesi R³'te yatmazlar ancak R4'e gömülebilirler. Topolojinin temel teoremlerinden biri, bir yüzeyi gömebilmek için en fazla 4 boyuta (R4) gerek olduğunu söyler.
Matematiksel tanım
İki boyutlu bir çokkatlıya yüzey denir. Daha ayrıntılı bir söyleyişle, (kenarı olmayan topolojik) yüzey, aşağıdaki koşulları sağlayan bir topolojik uzaydır:
Hausdorff'tur;
Herhangi bir noktasının çevresinde öyle bir açık komşuluk bulunabilir ki bu komşuluk R²'nin açık bir alt kümesine homeomorfiktir;
(Kimi tanımlarda) İkinci sayılabilirlik özelliğini sağlar;
(Kimi tanımlarda) Parakompakttır.
Yukarıki tanımda ikinci koşulda R² yerine, üst yarı düzlemi (yani ikinci koordinatları negatif olmayan noktaların kümesi) temsil etmek üzere H² konduğunda, bu tanım, kenarı olan (kenarlı) topolojik bir yüzey tanımına dönüşür. Bu durumda ikinci koşulda homeomorfizma sözcüğünün anlamlı olabilmesi için H² üzerinde bir topoloji bulunması gerekir. Bu topoloji standart olarak R²'den tetiklenen topolojidir.
Kenarı olan bir yüzeyin kenarı olmayandan farklı olarak şu tür noktaları da vardır: noktanın yeterince küçük her komşuluğu H²'de çapı yarı düzlemin en altında oturan bir yarım daireye homeomorfiktir. Noktanın R²'de açık bir bölgeye homeomorfik bir komşuluğu olması söz konusu değildir. Kenarlı yüzeylere birkaç örnek: düzlemde kapalı bir daire, kapalı bir eğriyle çevrelenmiş bir düzlem bölgesi, bir yarıküre (içi boş), açık bir dairesel parçası koparılmış bir simit (yüzeyi).
Bir yüzeyin içinde bir Möbius şeridi varsa (yüzeye gömülebiliyorsa) bu yüzeye yön verilemez denir. İçinde bir Möbius şeridi yoksa böyle bir yüzeye yön verilebilir denir. Yön verilemez yüzeylere birkaç örnek: Möbius şeridi, gerçel izdüşümsel düzlem, Klein şişesi. Bunlardan Möbius şeridi kenarı (bir çember) olan bir yüzeyken diğerleri kenarsız yüzeylerdir.
Yüzeylerin sınıflandırılması
Matematiğin temel uğraşlarından biri sınıflamadır. Tanımladığı bir nesne türünde, nesnelerin bazılarını bibirinden ayırdetmeden, olası tüm nesneleri listelemek sınıflamadaki amaçtır. Dolayısıyla yukarıda soyut tanımı verilen yüzeylerin tümünü listelemek, topolojinin ilgilendiği bir sorudur. Bunu yaparken iki homeomorfik yüzeyi bir tutar, bunların arasında ayrım gözetmez. Bu koşullar altında listeyi oluşturmaya çalışır. Örneğin bu listede (içi boş) bir küp ve bir küre birlikte görünmeyecektir; yalnızca biri listede yer alacaktır çünkü bu iki yüzey, R³'ten tetiklenen topolojileriyle birbirine homeomorfik yüzeylerdir.
Şu ve benzeri soruların yanıtlanması gerekir: bir küreyle bir simit birbirine homeomorfik midir? Möbius şeridiyle daire? Kenarı olan yüzeyle olmayan? Yön verilebilir olanla olmayan? vs.
Yüzeylerin sınıflandırılması problemi ilk kez August Ferdinand Möbius tarafından çalışılmış ve R³'te yatan yön verilebilir yüzeyler için 1870 yılında sonuç ilan edilmiştir. Max Wilhelm Dehn ve P. Heegard 1907 yılında üçgenlenebilir yüzeyler için tüm sınıflandırmayı vermiştir. Her topolojik yüzeyin üçgenlenebilir olduğunu 1925 yılında Tibor Radó ispatlayarak sınıflandırmayı sona erdirmiştir (ispat için L.V.Ahlfors ve L.Sario'nun aşağıda listelenmiş kitabına bakınız).
Bu sınıflandırmaya göre, tıkız, yön verilebilir, kenarsız yüzeyler şunlardan biri(ne homeomorfik) olmak zorundadır:
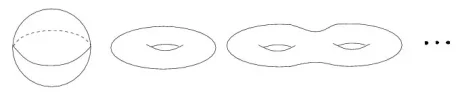
İlk şekil bir küredir (S²). İkincisi bir simit (T²). Üçüncü şekil çift delikli bir yüzeyi (F²) anlatır. Listede sırasıyla 3, 4, 5 ,... delikli yüzeyler (sırasıyla F3, F4, F5, ...) yer alacaktır. Dikkat edilirse, iki ayrı simitten birer daire oyulup kalan yüzeyler birbirlerine yapıştırılırsa, çıkan yüzey, iki delikli bir yüzey olacaktır. Üzerindeki topoloji, bu yapıştırma sırasında kullanılan özdeşleştirme aracılığıyla gelen bölüm topolojisidir. Bu işlem şöyle gösterilir:
F2 = T² # T²
Daireler oyarak yapıştırma işlemine bağlantılı toplam denir. Üç delikli bir yüzey, çift delikli bir yüzeyle torusun bağlantılı toplamı olarak inşa edilebilir.
Bu sınıflandırmadan anlaşılıyor ki, tıkız, yön verilebilir, kenarsız yüzeyler delik sayılarıyla anlatılabilirler. Kürenin delik sayısına 0 diyoruz. Simidin delik sayısı 1'dir.
Tıkız, yön verilebilir, kenarsız S adlı bir yüzey için 2 - 2g sayısı yüzeyin Euler sayısına eşittir ve şöyle gösterilir:
χ(S) = 2 − 2g.
Yön verilemez yüzeyler için sınıflandırmaysa temelde aynı olmasına karşın, söz konusu yüzeylere daha az aşinayız. Tıkız, yön verilemez, kenarsız yüzeylerin en basiti gerçel izdüşümsel düzlemdir (RP²). Bu yüzey, bir Möbius şeridiyle bir dairenin kenarlarından birbirlerine yapıştırılmasıyla inşa edilir. Üzerindeki topoloji, bu yapıştırma aracılığıyla gelen bölüm topolojisidir. İki tane RP²'nin bağlantılı toplamına Klein şişesi (K²) denir:
K² = RP² # RP²
Bu işlem iki Möbius şeridinin kenarlarından birbirlerine yapıştırılmasından başka bir şey değildir.
Sınıflandırma şunu söyler: tıkız, yön verilemez, kenarsız yüzeyler aşağıdakilerden biri(ne homeomorfik) olmak zorundadır:
RP², K² = RP² # RP², (RP² # RP² # RP²), (RP² # RP² # RP² # RP²),
Gösterilebilir ki bu listedeki yüzeylerin Euler sayıları 1'den başlar ve birer birer azalır:
χ(RP2) = 1
Dolayısıyla, (tıkız, kenarsız) bir yüzeyin Euler sayısını ve yön verilebilir mi değil mi olduğunu söylemek, yüzeyi anlatmaya yeter.
Yüzey, matematikte ve özellikle topolojide iki boyutlu çokkatlı. İki gerçel değişkenli ve gerçel değerli bir fonksiyonun üç boyutlu uzayda (R³) grafiği tipik yüzey örneğidir. Ayrıca dünya yüzeyi, bir yumurtanın kabuğu, bir simit birer yüzeydir.
Bir yüzeyin 2 boyutlu bir çokkatlı olması, öncelikle onun (belirli özellikleri sağlayan) bir topolojik uzay olması demektir. Bunun yanında yüzeyin verilen (herhangi) bir x noktası çevresinde öyle bir komşuluk bulunabilir ki, bu komşuluk 2 boyutlu uzayın bir parçasına benzer. Bu komşuluğa yama denir. Bu benzeme uyarınca, x çevresinde sağ-sol ve yukarı-aşağı kavramları iyi bir biçimde tanımlanabilir. Daha iyi bir deyişle, x'in çevresine bir koordinat sistemi döşenebilir. Böylece yüzey, bir düzlem parçası olmasa bile x çevresindeki noktalar bir düzlemdeymiş gibi koordinatlara sahip olur.
Dünya yüzeyi matematiksel olarak bir yüzeydir. Dünyanın çizilen her haritası, yukarıdaki anlamda bir koordinat sistemi tarif eder. Bu sayede denizcilikte yön bulma kolaylaşır ve iki denizci aynı koordinat sisteminde konuşarak birbirleriyle anlaşabilir. Dünya yüzeyi için standart koordinat sistemi, enlem ve boylamlarla verilir. Örneğin, dünya yüzeyinden gün dönümü çizgisi ve kutuplar silindiğinde kalan parçaya (180^{\circ} Doğu, 180^{\circ} Batı) ila (90^{\circ} Kuzey, 90^{\circ} Güney) koordinatları verilerek bu parça bir yamaya dönüştürülebilir. Gün dönümü çizgisi ya da kutupların silinmediği durumda bazı enlem-boylam çiftlerinin aynı noktayı tarif edeceklerine dikkat ediniz.
Topolojik bir yüzey, her zaman R³'te görülemeyebilir. Örneğin gerçel izdüşümsel düzlem ya da Klein şişesi R³'te yatmazlar ancak R4'e gömülebilirler. Topolojinin temel teoremlerinden biri, bir yüzeyi gömebilmek için en fazla 4 boyuta (R4) gerek olduğunu söyler.
Matematiksel tanım
İki boyutlu bir çokkatlıya yüzey denir. Daha ayrıntılı bir söyleyişle, (kenarı olmayan topolojik) yüzey, aşağıdaki koşulları sağlayan bir topolojik uzaydır:
Hausdorff'tur;
Herhangi bir noktasının çevresinde öyle bir açık komşuluk bulunabilir ki bu komşuluk R²'nin açık bir alt kümesine homeomorfiktir;
(Kimi tanımlarda) İkinci sayılabilirlik özelliğini sağlar;
(Kimi tanımlarda) Parakompakttır.
Yukarıki tanımda ikinci koşulda R² yerine, üst yarı düzlemi (yani ikinci koordinatları negatif olmayan noktaların kümesi) temsil etmek üzere H² konduğunda, bu tanım, kenarı olan (kenarlı) topolojik bir yüzey tanımına dönüşür. Bu durumda ikinci koşulda homeomorfizma sözcüğünün anlamlı olabilmesi için H² üzerinde bir topoloji bulunması gerekir. Bu topoloji standart olarak R²'den tetiklenen topolojidir.
Kenarı olan bir yüzeyin kenarı olmayandan farklı olarak şu tür noktaları da vardır: noktanın yeterince küçük her komşuluğu H²'de çapı yarı düzlemin en altında oturan bir yarım daireye homeomorfiktir. Noktanın R²'de açık bir bölgeye homeomorfik bir komşuluğu olması söz konusu değildir. Kenarlı yüzeylere birkaç örnek: düzlemde kapalı bir daire, kapalı bir eğriyle çevrelenmiş bir düzlem bölgesi, bir yarıküre (içi boş), açık bir dairesel parçası koparılmış bir simit (yüzeyi).
Bir yüzeyin içinde bir Möbius şeridi varsa (yüzeye gömülebiliyorsa) bu yüzeye yön verilemez denir. İçinde bir Möbius şeridi yoksa böyle bir yüzeye yön verilebilir denir. Yön verilemez yüzeylere birkaç örnek: Möbius şeridi, gerçel izdüşümsel düzlem, Klein şişesi. Bunlardan Möbius şeridi kenarı (bir çember) olan bir yüzeyken diğerleri kenarsız yüzeylerdir.
Yüzeylerin sınıflandırılması
Matematiğin temel uğraşlarından biri sınıflamadır. Tanımladığı bir nesne türünde, nesnelerin bazılarını bibirinden ayırdetmeden, olası tüm nesneleri listelemek sınıflamadaki amaçtır. Dolayısıyla yukarıda soyut tanımı verilen yüzeylerin tümünü listelemek, topolojinin ilgilendiği bir sorudur. Bunu yaparken iki homeomorfik yüzeyi bir tutar, bunların arasında ayrım gözetmez. Bu koşullar altında listeyi oluşturmaya çalışır. Örneğin bu listede (içi boş) bir küp ve bir küre birlikte görünmeyecektir; yalnızca biri listede yer alacaktır çünkü bu iki yüzey, R³'ten tetiklenen topolojileriyle birbirine homeomorfik yüzeylerdir.
Şu ve benzeri soruların yanıtlanması gerekir: bir küreyle bir simit birbirine homeomorfik midir? Möbius şeridiyle daire? Kenarı olan yüzeyle olmayan? Yön verilebilir olanla olmayan? vs.
Yüzeylerin sınıflandırılması problemi ilk kez August Ferdinand Möbius tarafından çalışılmış ve R³'te yatan yön verilebilir yüzeyler için 1870 yılında sonuç ilan edilmiştir. Max Wilhelm Dehn ve P. Heegard 1907 yılında üçgenlenebilir yüzeyler için tüm sınıflandırmayı vermiştir. Her topolojik yüzeyin üçgenlenebilir olduğunu 1925 yılında Tibor Radó ispatlayarak sınıflandırmayı sona erdirmiştir (ispat için L.V.Ahlfors ve L.Sario'nun aşağıda listelenmiş kitabına bakınız).
Bu sınıflandırmaya göre, tıkız, yön verilebilir, kenarsız yüzeyler şunlardan biri(ne homeomorfik) olmak zorundadır:

İlk şekil bir küredir (S²). İkincisi bir simit (T²). Üçüncü şekil çift delikli bir yüzeyi (F²) anlatır. Listede sırasıyla 3, 4, 5 ,... delikli yüzeyler (sırasıyla F3, F4, F5, ...) yer alacaktır. Dikkat edilirse, iki ayrı simitten birer daire oyulup kalan yüzeyler birbirlerine yapıştırılırsa, çıkan yüzey, iki delikli bir yüzey olacaktır. Üzerindeki topoloji, bu yapıştırma sırasında kullanılan özdeşleştirme aracılığıyla gelen bölüm topolojisidir. Bu işlem şöyle gösterilir:
F2 = T² # T²
Daireler oyarak yapıştırma işlemine bağlantılı toplam denir. Üç delikli bir yüzey, çift delikli bir yüzeyle torusun bağlantılı toplamı olarak inşa edilebilir.
Bu sınıflandırmadan anlaşılıyor ki, tıkız, yön verilebilir, kenarsız yüzeyler delik sayılarıyla anlatılabilirler. Kürenin delik sayısına 0 diyoruz. Simidin delik sayısı 1'dir.
Tıkız, yön verilebilir, kenarsız S adlı bir yüzey için 2 - 2g sayısı yüzeyin Euler sayısına eşittir ve şöyle gösterilir:
χ(S) = 2 − 2g.
Yön verilemez yüzeyler için sınıflandırmaysa temelde aynı olmasına karşın, söz konusu yüzeylere daha az aşinayız. Tıkız, yön verilemez, kenarsız yüzeylerin en basiti gerçel izdüşümsel düzlemdir (RP²). Bu yüzey, bir Möbius şeridiyle bir dairenin kenarlarından birbirlerine yapıştırılmasıyla inşa edilir. Üzerindeki topoloji, bu yapıştırma aracılığıyla gelen bölüm topolojisidir. İki tane RP²'nin bağlantılı toplamına Klein şişesi (K²) denir:
K² = RP² # RP²
Bu işlem iki Möbius şeridinin kenarlarından birbirlerine yapıştırılmasından başka bir şey değildir.
Sınıflandırma şunu söyler: tıkız, yön verilemez, kenarsız yüzeyler aşağıdakilerden biri(ne homeomorfik) olmak zorundadır:
RP², K² = RP² # RP², (RP² # RP² # RP²), (RP² # RP² # RP² # RP²),
Gösterilebilir ki bu listedeki yüzeylerin Euler sayıları 1'den başlar ve birer birer azalır:
χ(RP2) = 1
Dolayısıyla, (tıkız, kenarsız) bir yüzeyin Euler sayısını ve yön verilebilir mi değil mi olduğunu söylemek, yüzeyi anlatmaya yeter.