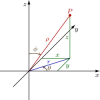İntegral hesaplama
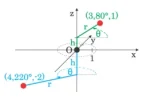
0 < b − a < 2π olmak üzere, r(θ) eğrisinin [a, b] kapalı aralığında kalan kısmının altında kalan alanı bulmak için, öncelikle eğri bir Riemann toplamı olarak tanımlanır.
* İlk olarak, [a, b] aralığı n kadar alt aralığa bölünür (burada n, isteğe bağlı seçilmiş pozitif bir tam sayıdır). Böylece, her alt aralığın uzunluğunu temsil eden Δθ, aralığın tüm uzunluğunun (b − a) alt aralık sayısına (n) bölümüne eşit olur.
* Her i = 1, 2, , n alt aralığı için θi'nin alt aralığın orta noktası olduğu kabul edilir ve merkezi kutupta, yarıçapı r(θi) ve merkezî açısı Δθ olan birer sektör çizilir.
* Buna göre, çizilmiş her sektörün alanı şu denklemle verilebilir:

Dolayısıyla, tüm sektörlerin toplam alanı da altta sunulan denklemle tanımlanır:

n alt aralıklarının sayısı ne kadar artarsa, söz konusu alanın ölçümü de gerçek alana o kadar çok yaklaşır. Böylece, [a, b] aralığındaki r(θ) eğrisinin altında kalan alan söyle tanımlanabilir:

Bu ifade, aşağıdaki integralin Riemann toplamıdır:

0 < b − a < 2π olmak üzere, r(θ) eğrisinin [a, b] kapalı aralığında kalan kısmının altında kalan alanı bulmak için, öncelikle eğri bir Riemann toplamı olarak tanımlanır.
* İlk olarak, [a, b] aralığı n kadar alt aralığa bölünür (burada n, isteğe bağlı seçilmiş pozitif bir tam sayıdır). Böylece, her alt aralığın uzunluğunu temsil eden Δθ, aralığın tüm uzunluğunun (b − a) alt aralık sayısına (n) bölümüne eşit olur.
* Her i = 1, 2, , n alt aralığı için θi'nin alt aralığın orta noktası olduğu kabul edilir ve merkezi kutupta, yarıçapı r(θi) ve merkezî açısı Δθ olan birer sektör çizilir.
* Buna göre, çizilmiş her sektörün alanı şu denklemle verilebilir:
Dolayısıyla, tüm sektörlerin toplam alanı da altta sunulan denklemle tanımlanır:

n alt aralıklarının sayısı ne kadar artarsa, söz konusu alanın ölçümü de gerçek alana o kadar çok yaklaşır. Böylece, [a, b] aralığındaki r(θ) eğrisinin altında kalan alan söyle tanımlanabilir:

Bu ifade, aşağıdaki integralin Riemann toplamıdır: